Question

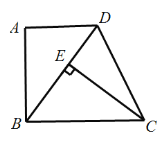
【题目】如图，在△ABC中，AB＝AC，AB的垂直平分线交AB于N，交AC于M．

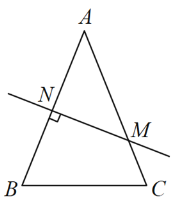
（1）若∠C ＝70°，求的度数；

（2）若∠C ＝α，请用含α的式子表示；

（3）连接MB，若AB ＝8，BC ＝6．

①求△的周长；

②在直线上是否存在点P，使（PB+CP）的值最小？若存在，标出点P的位置并求（PB+CP）的最小值；若不存在，说明理由．

Answer 1

【答案】（1） ；（2）∠NMA＝2α﹣90° ；（3） ①14；②当点P与点M重合时，PB+CP的值最小，最小值是8.

【解析】

（1）根据等腰三角的性质，三角形的内角和定理，可得∠A的度数，根据直角三角形两锐角的关系，可得答案；

（2）根据等腰三角的性质，三角形的内角和定理，可得∠A的度数，根据直角三角形两锐角的关系，可得答案；

（3）①根据垂直平分线的性质，可得AM与MB的关系，再根据三角形的周长，可得答案；②根据两点之间线段最短，可得P点与M点的关系，可得PB+PC与AC的关系

解：（1）∵AB＝AC，且∠C=70°，

∴∠B=∠C=70°,∠A=40°

又∵AB的垂直平分线交AB于N

∴∠NMA=90°-40°= 50°，

故答案为：50°；
（2）∵AB＝AC，且∠C=α，

∴∠B=∠C=α,∠A=

又∵AB的垂直平分线交AB于N

∴∠NMA=90°-=°，

（3）如图：连接BM

MN垂直平分AB．

∴MB=MA，

∴△MBC的周长为BM+CM+BC=AM+CM+BC=AC+BC

又∵AB=AC

∴AC+BC=AB+BC=14cm，

∴∴△MBC的周长为14cm.

存在.当点P与点M重合时，PB+CP的值最小，最小值是8cm．