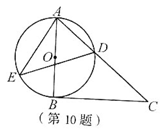
题目内容
如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.

(1)求证:OF∥BC;(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD= cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.

(1)求证:OF∥BC;(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=
 cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.(1)证明:∵AB为⊙O的直径,
∴AC⊥BC
又∵OF⊥AC
∴OF∥BC
(2)证明:∵AB⊥CD
∴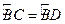
∴∠CAB=∠BCD
又∵∠AFO=∠CEB=90°,OF=BE,
∴△AFO≌△CEB
(3)∵AB⊥CD
∴CE=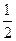 CD=
CD=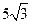 cm.
cm.
在直角△OCE中,OC=OB=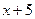 (cm),
(cm),
根据勾股定理可得: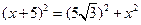
解得: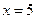
∴tan∠COE=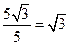
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是: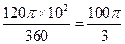 cm2
cm2
△COD的面积是: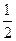 CD•OE=
CD•OE=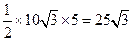 cm2
cm2
∴阴影部分的面积是: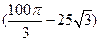 cm2.
cm2.
∴AC⊥BC
又∵OF⊥AC
∴OF∥BC
(2)证明:∵AB⊥CD
∴
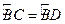
∴∠CAB=∠BCD
又∵∠AFO=∠CEB=90°,OF=BE,
∴△AFO≌△CEB
(3)∵AB⊥CD
∴CE=
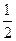 CD=
CD=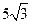 cm.
cm.在直角△OCE中,OC=OB=
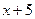 (cm),
(cm),根据勾股定理可得:
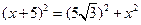
解得:
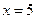
∴tan∠COE=
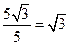
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是:
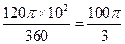 cm2
cm2△COD的面积是:
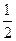 CD•OE=
CD•OE=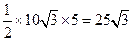 cm2
cm2∴阴影部分的面积是:
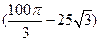 cm2.
cm2.略

练习册系列答案
相关题目
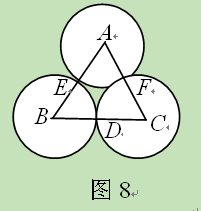
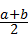 与
与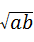 的大小关系是
的大小关系是 ●探究证明
●探究证明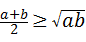 .
.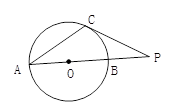 ∠BAC=30°,过点C作⊙O的切线交AB的延长线于点
∠BAC=30°,过点C作⊙O的切线交AB的延长线于点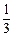 ,求DE的长.
,求DE的长.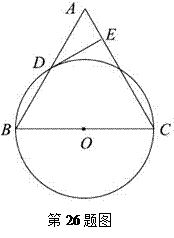
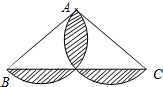
 48 B、25π﹣48 C、50π﹣24 D、
48 B、25π﹣48 C、50π﹣24 D、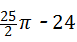
 ,∠COD=60°.
,∠COD=60°.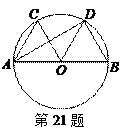

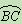 上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连结AD、BD、
上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连结AD、BD、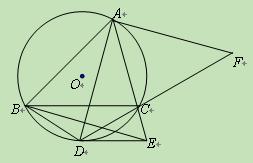
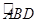 上异于点A、D的一点.若∠C=40°,则∠E的度数为 .
上异于点A、D的一点.若∠C=40°,则∠E的度数为 .