题目内容
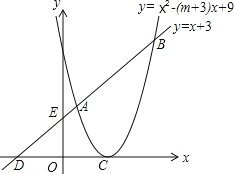
【题目】如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标.
【答案】(1)3;(2)A点的坐标是(1,4),B两点的坐标是(6,9).
【解析】
(1)根据抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,可得抛物线与x轴只有一个交点,所以△=0,据此求出m的值是多少即可.
(2)联立抛物线与一次函数的解析式,求出A、B两点的坐标各是多少即可.
(1)∵抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,
∴抛物线与x轴只有一个交点,
∴(m+3)2-4×9=0,
解得m=3或m=-9,
又∵-![]() >0,
>0,
∴m>-3,
∴m=3.
(2)由(1),可得m=3,
∴抛物线的解析式为:y=x2-6x+9,
联立![]()
解得![]() 或
或![]() ,
,
根据图示,可得A点的横坐标小于B点的横坐标,
∴A点的坐标是(1,4),B两点的坐标是(6,9).

练习册系列答案
相关题目
【题目】问题: 探究![]() 的图象与性质
的图象与性质
操作:(1)请在横线上补充完整表格:
… | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … | |
… | - |
|
|
|
| 0 | - | - |
|
| … |
(2)请在图中根据剩余的点补全此函数的图象;
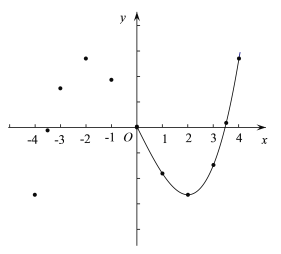
发现:写出该函数图像的一条性质 ;
应用:(1)方程![]() 实数根的个数为 个;
实数根的个数为 个;
(2)![]() 的解集为 .
的解集为 .
【题目】小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 | 购买数量(件 | 购买总费用(元 | |
A | B | ||
第一次 | 2 | 1 | 55 |
第二次 | 1 | 3 | 65 |
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.