��Ŀ����
����Ŀ��̽��
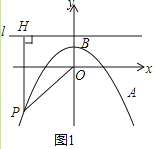
����1 ��֪����ͼ1��������ABC�У���D��AB�ߵ��е㣬AE��BC��BF��AC������ֱ�Ϊ��E��F��AE��BF���ڵ�M������DE��DF����DE=kDF����k��ֵΪ�� ����
��չ
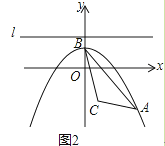
����2 ��֪����ͼ2��������ABC�У�CB=CA����D��AB�ߵ��е㣬��M��������ABC���ڲ�������MAC=��MBC������M�ֱ���ME��BC��MF��AC������ֱ�Ϊ��E��F������DE��DF����֤��DE=DF��
�ƹ�
����3 ��ͼ3��������������2�е�������CB=CA����Ϊ��CB��CA���������������䣬��̽��DE��DF֮���������ϵ����֤����Ľ��ۣ�

���𰸡���1��1����2��֤������������3��DE=DF�����ɼ�����.
��������
��1������ֱ�������ε����ʡ�ֱ��������б�����ߵ���б�ߵ�һ�롱�õ�DE=DF��
��2�����õ��������ε����ʺ��ж��ó����ۣ��Ӷ��ж���MEB�ա�MFA��AAS�����õ�DE=DF��
��3�����������ε���λ�ߺ�ֱ�������ε����ʸ���SAS֤����DHE�ա�FGD�ɵã�
��1����AE��BC��BF��AC
���AEB����AFB����ֱ��������
��D��AB���е�
��DE��DF�ֱ�ΪRt��AEB��Rt��AFB��б������
��DE=![]() AB��DF=
AB��DF=![]() AB��ֱ��������б�����ߵ���б�ߵ�һ�룩
AB��ֱ��������б�����ߵ���б�ߵ�һ�룩
��DE=DF
��DE=kDF
��k=1
��2����CB=CA
���CBA=��CAB
�ߡ�MAC=��MB
���CBA����MBC=��CAB����MAC
����ABM=��BAM
��AM=BM
��ME��BC��MF��AC
���MEB=��MFA=90
���ߡ�MBE=��MAF
���MEB�ա�MFA��AAS��
��BE=AF
��D��AB���е㣬��BD=AD
���ߡ�DBE=��DAF
���DBE�ա�DAF��SAS��
��DE=DF
��3��DE=DF
��ͼ1����AM���е�G��BM���е�H��
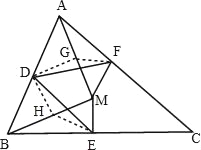
���� D�� �� AB�� �е�
��DG��BM��DG=![]() BM
BM
ͬ���ɵã�DH��AM��DH=![]() AM
AM
��ME��BC��E��H ��BM���е�
����Rt��BEM��HE=![]() BM=BH
BM=BH
���HBE=��HEB
��MHE=��HBE+��HEB=2��MBC
����DG=![]() BM��HE=
BM��HE=![]() BM
BM
��DG=HE
ͬ���ɵã�DH=FG����MGF=2��MAC
��DG��BM��DH��GM
���ı���DHMG��ƽ���ı���
���DGM=��DHM
�ߡ�MGF=2��MAC����MHE=2��MBC
���ߡ�MBC=��MAC
���MGF=��MHE
���DGM+��MGF=��DHM+��MHE
���DGF=��DHE
����DHE����FGD��
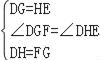 ��
��
���DHE�ա�FGD��SAS����
��DE=DF