题目内容
【题目】已知直线m，n相交于点B，点A，C分别为直线m，n上的点，AB=BC=1，且∠ABC=60°，点E是直线m上的一个动点，点D是直线n上的一个动点，运动过程中始终满足DE=CE．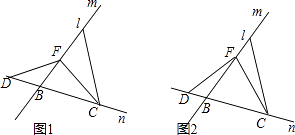 
（1）如图1，当点E运动到线段AB的中点，点D在线段CB的延长线上时，求BD的长．
（2）如图2，当点E在线段AB上运动，点D在线段CB的延长线上时，试确定线段BD与AE的数量关系，并说明理由．
【答案】
（1）解：∵∠ABC=60°，AB=BC，
∴△ABC为等边三角形，
∴∠ACB=60°，
∵点E是线段AB的中点，
∴∠ECB= 
∠ACB=30°，
∵DE=CE，
∴∠EDB=∠ECB=30°，
∵∠ABC=∠EDB+∠DEB，
∴∠DEB=30°=∠EDB，
∴BD=DE= AB=
（2）解：BD=AE；理由如下：
过点E作EF∥BC交AC于点F，如图所示：
∵EF∥BC，
∴∠AFE=∠ACB=60°，
∴∠EFC=120°，∠AFE=∠A，
∴EF=EA，
∵∠ABC=60°，
∴∠EBD=120°，
∴∠EFC=∠EBD，
∵CE=DE，
∴∠EDB=∠ECB，
∵∠EDB+∠DEB=∠ECB+∠ECF=60°，
∴∠DEB=∠ECF，
在△EDB和△CEF中，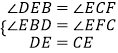 
，
∴△EDB≌△CEF（AAS），
∴BD=EF，
∵EF=EA，
∴BD=AE．
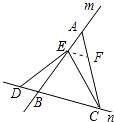
【解析】（1）证明△ABC为等边三角形，得出∠ACB=∠ABC=60°，由等边三角形的性质得出∠ECB= ∠ACB=30°，由等腰三角形的性质得出∠EDB=30°，由三角形的外角性质得出∠DEB=∠EDB，即可得出结论；（2过点E作EF∥BC交AC于点F，由平行线的性质得出∠AFE=∠ACB=60°，证出∠EFC=120°，∠AFE=∠A，得出EF=EA，证出∠DEB=∠ECF，由AAS证明△EDB≌△CEF，得出BD=EF，即可得出结论．
