Question

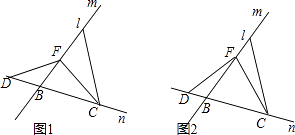
【题目】如图，在△ABC中，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得到△CFE ．

（1）求证：四边形ADCF是平行四边形．
（2）当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．

Answer 1

【答案】
（1）

解答：证明：∵△CFE是由△ADE绕点E旋转180°得到，

∴点A、E、C三点共线，点D、E、F三点共线，且AE＝CE，DE＝FE，故四边形ADCF是平行四边形．

（2）

解答：解：当∠ACB＝90°，AC＝BC时，四边形ADCF是正方形．

理由如下：在△ABC中，∵AC＝BC，AD＝BD，点D是边AB的中点，

∴CD⊥AB，即∠ADC＝90°，

而由（1）知，四边形ADCF是平行四边形，

∴四边形ADCF是矩形．

又∵∠ACB＝90°，

∴CD＝ AB＝AD，

故四边形ADCF是正方形．

【解析】（1）利用旋转的性质得出点A、E、C三点共线，点D、E、F三点共线，且AE＝CD ， DE＝FE ， 即可得出答案；（2）首先得出CD⊥AB ， 即∠ADC＝90°，由（1）知，四边形ADCF是平行四边形，故四边形ADCF是矩形．进而求出CD＝AD即可得出答案．
【考点精析】本题主要考查了平行四边形的判定和正方形的判定方法的相关知识点，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形；先判定一个四边形是矩形，再判定出有一组邻边相等；先判定一个四边形是菱形，再判定出有一个角是直角才能正确解答此题．