Question

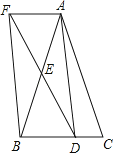
【题目】如图，在△ABC中，点O在AB边上，过点O作BC的平行线交∠ABC的平分线于点D ， 过点B作BE⊥BD交直线OD于点E ．

（1）求证：OE＝OD；
（2）当点O在AB的什么位置时，四边形BDAE是矩形？说明理由．

Answer 1

【答案】
（1）

解答：证明：∵BD是∠ABC的角平分线，

∴∠ABD＝∠DBC；∵ED∥BC，

∴∠ODB＝∠DBC＝∠ABD，

∴△OBD为等腰三角形，

∴OB＝OD，在Rt△EBD中，OB＝OD，那么O就是斜边ED的中点．

∴OE＝OD．

（2）

解答：O为AB的中点时，四边形BDAE为矩形

∵四边形BDAE为矩形，

∴∠AEB为直角即△AEB为直角三角形，OA＝OB＝OE＝OD，

∵Rt△AEB中，OE＝OA＝OB，

∴O为斜边AB的中点，

∴O为AB的中点时，四边形BDAE为矩形．

【解析】（1）根据角平分线和等腰三角形腰长相等性质证明OB＝OD ， 再根据直角三角形中线的性质即可判定O点为DE的中点，即OE＝OD；（2）设定四边形BDAE为矩形，可求出Rt△AEB中，O点为斜边AB的中点.
【考点精析】通过灵活运用直角三角形斜边上的中线和矩形的判定方法，掌握直角三角形斜边上的中线等于斜边的一半；有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形即可以解答此题．