Question

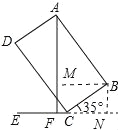
【题目】如图1是一个新款水杯，水杯不盛水时按如图2所示的位置放置，这样可以快速晾干杯底，干净透气；将图2的主体部分的抽象成图3，此时杯口与水平直线的夹角为35°，四边形ABCD可以看作矩形，测得AB=10cm，BC=8cm，过点A作AF⊥CE，交CE于点F．

（1）求∠BAF的度数；

（2）求点A到水平直线CE的距离AF的长（精确到0.1cm）

（参考数据sin35°≈0.5736，cos35°≈0.8192，tan35°≈0.7002）

Answer 1

【答案】（1）35°；（2）12.8cm．

【解析】

试题分析：（1）∠D=∠BCD=90°，求出∠DAF=∠DCE=55°，即可得出结果；（2）作BM⊥AF于M，BN⊥EF于N，由三角函数得出MF=BN=BCsin35°≈4.59（cm），AM=ABcos35°≈8.20，（cm），即可得出结果．

试题解析：（1）∵四边形ABCD是矩形，∴∠D=∠BCD=90°，∴∠DAF=∠DCE=90°﹣35°=55°，∴∠BAF=90°﹣55°=35°；（2）作BM⊥AF于M，BN⊥EF于N，如图所示：则MF=BN=BCsin35°=0.5736×8≈4.59（cm），

AM=ABcos35°=10×0.8192≈8.20，（cm），∴AF=AM+MF=8.20+4.59≈12.8（cm）；即A到水平直线CE的距离AF的长为12.8cm．