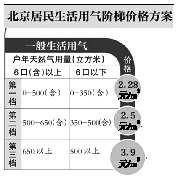
题目内容
【题目】如图，在Rt△ABC中，∠ACB=90°，D、E分别为AB，AC边上的中点，连接DE，将△ADE绕点E旋转180°得到△CFE，连接AF，AC．
（1）求证：四边形ADCF是菱形；
（2）若BC=8，AC=6，求四边形ABCF的周长．
【答案】（1）证明见解析；（2）28．
【解析】试题分析：（1）根据旋转可得AE=CE，DE=EF，可判定四边形ADCF是平行四边形，然后证明DF⊥AC，可得四边形ADCF是菱形；
（2）首先利用勾股定理可得AB长，再根据中点定义可得AD=5，根据菱形的性质可得AF=FC=AD=5，进而可得答案．
试题解析：（1）∵将△ADE绕点E旋转180°得到△CFE，
∴AE=CE，DE=EF，
∴四边形ADCF是平行四边形，
∵D、E分别为AB，AC边上的中点，
∴DE是△ABC的中位线，
∴DE∥BC，
∵∠ACB=90°，
∴∠AED=90°，
∴DF⊥AC，
∴四边形ADCF是菱形；
（2）在Rt△ABC中，BC=8，AC=6，
∴AB=10，
∵D是AB边上的中点，
∴AD=5，
∵四边形ADCF是菱形，
∴AF=FC=AD=5，
∴四边形ABCF的周长为8+10+5+5=28．
练习册系列答案
相关题目
【题目】为了保护环境，某开发区综合治理指挥部决定购买A，B两种型号的污水处理设备共10台．已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同，每台设备价格及月处理污水量如下表所示：
污水处理设备 | A型 | B型 |
价格（万元/台） | m | m﹣3 |
月处理污水量（吨/台） | 220 | 180 |
（1）求m的值；
（2）由于受资金限制，指挥部用于购买污水处理设备的资金不超过165万元，问有多少种购买方案？并求出每月最多处理污水量的吨数．
