题目内容
【题目】如图,已知矩形ABCD满足AB:BC=1: ![]() ,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )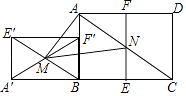
A.4 ![]()
B.4
C.2
D.1
【答案】C
【解析】解:由折叠可得,BE= ![]() BC=AF,而AB:BC=1:
BC=AF,而AB:BC=1: ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
由旋转可得,AF=A'E',AB=A'B,
∴ ![]() =
= ![]() ,
,
又∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
又∵∠E'A'B=∠ABC=90°,
∴△E'A'B∽△ABC,
∴∠A'BE'=∠ACB,
∴AC∥BE',
连接BN,则△AMN的面积=△ABN的面积,
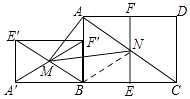
由题可得,N为AC的中点,故△ABN的面积为△ABC面积的一半,
∴△AMN的面积为△ABC面积的一半,即矩形ABCD面积的四分之一,
∴△AMN的面积= ![]() ×8=2,
×8=2,
所以答案是:C.
【考点精析】解答此题的关键在于理解平行线之间的距离的相关知识,掌握两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目