题目内容
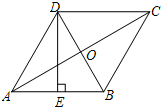
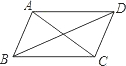
在四边形ABCD中,AC、BD交于O点,且AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.
(1)说明四边形ABCD为什么是菱形;
(2)过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E,判断四边形OBEC的形状,并说明理由.

(1)说明四边形ABCD为什么是菱形;
(2)过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E,判断四边形OBEC的形状,并说明理由.

(1)∵AC平分∠DAB和∠DCB,
∴∠DAC=∠BAC,∠DCA=∠BCA,
在△DAC和△BAC中
∴△DAC≌△BAC,
∴AD=AB,DC=BC,
同理△ADB≌△CDB,
∴AD=DC,
即AD=DC=BC=AB,
∴四边形ABCD是菱形.
(2)四边形OBEC是矩形,
理由是:∵CE∥DB,BE∥AC,
∴四边形OBEC是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COB=90°,
∴平行四边形OBEC是矩形.
∴∠DAC=∠BAC,∠DCA=∠BCA,
在△DAC和△BAC中
|
∴△DAC≌△BAC,
∴AD=AB,DC=BC,
同理△ADB≌△CDB,
∴AD=DC,
即AD=DC=BC=AB,
∴四边形ABCD是菱形.
(2)四边形OBEC是矩形,
理由是:∵CE∥DB,BE∥AC,
∴四边形OBEC是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COB=90°,
∴平行四边形OBEC是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目