Question

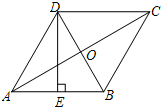
如图，在菱形ABCD中，AC，BD相交于点O，E为AB的中点，DE⊥AB．
（1）求∠ABC的度数；
（2）如果AC=4

3

，求DE的长．

Answer 1

（1）∵E为AB的中点，DE⊥AB，
∴AD=DB，
∵四边形ABCD是菱形，
∴AB=AD，
∴AD=DB=AB，
∴△ABD为等边三角形．
∴∠DAB=60°．
∵菱形ABCD的边AD∥BC，
∴∠ABC=180°-∠DAB=180°-60°=120°，
即∠ABC=120°；

（2）∵四边形ABCD是菱形，
∴BD⊥AC于O，AO=

1

2

AC=

1

2

×4

3

=2

3

，
由（1）可知DE和AO都是等边△ABD的高，
∴DE=AO=2

3

．