题目内容
 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5.DE⊥CD,且DE=CD,连AE,则△ADE的面积为
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5.DE⊥CD,且DE=CD,连AE,则△ADE的面积为
- A.1
- B.2
- C.3
- D.4
C
分析:连接EC,作DF⊥BC交BC于点F,作EH⊥AD交AD的延长线于H;通过证明可得∠EDH=∠FDC,由已知∠EHD=∠DFC=90°,且DE=CD,可推得△EHD≌△CFD,从而可得EH=FC;在三角形DFC中据AD=3,BC=5可得FC的长为2;所以△ADE的面积为 AD×EH=3.
AD×EH=3.
解答: 解:如图,作DF⊥BC交BC于点F,作EH⊥AD交AD的延长线于H,
解:如图,作DF⊥BC交BC于点F,作EH⊥AD交AD的延长线于H,
∵∠EDH+∠HDC=90°,∠HDC+∠CDF=90°,∴∠EDH=∠CDF;
又∵∠EHD=∠CFD=90°,且ED=CD,
∴△EHD≌△CFD,即CF=EH;
在直角梯形中AD∥BC,AB⊥BC,DF⊥BC,AD=3,BC=5,
∴AD=BF=3,则CF=BC-BF=5-3=2,即CF=EH=2;
∴△ADE在面积= AD×EH=
AD×EH= ×3×2=3.
×3×2=3.
故选C.
点评:此题解题的关键在于正确画出辅助线,涉及到三角形全等、直角梯形的性质等相关知识,是一道考查学生综合应用能力的好题.
分析:连接EC,作DF⊥BC交BC于点F,作EH⊥AD交AD的延长线于H;通过证明可得∠EDH=∠FDC,由已知∠EHD=∠DFC=90°,且DE=CD,可推得△EHD≌△CFD,从而可得EH=FC;在三角形DFC中据AD=3,BC=5可得FC的长为2;所以△ADE的面积为
 AD×EH=3.
AD×EH=3.解答:
 解:如图,作DF⊥BC交BC于点F,作EH⊥AD交AD的延长线于H,
解:如图,作DF⊥BC交BC于点F,作EH⊥AD交AD的延长线于H,∵∠EDH+∠HDC=90°,∠HDC+∠CDF=90°,∴∠EDH=∠CDF;
又∵∠EHD=∠CFD=90°,且ED=CD,
∴△EHD≌△CFD,即CF=EH;
在直角梯形中AD∥BC,AB⊥BC,DF⊥BC,AD=3,BC=5,
∴AD=BF=3,则CF=BC-BF=5-3=2,即CF=EH=2;
∴△ADE在面积=
 AD×EH=
AD×EH= ×3×2=3.
×3×2=3.故选C.
点评:此题解题的关键在于正确画出辅助线,涉及到三角形全等、直角梯形的性质等相关知识,是一道考查学生综合应用能力的好题.

练习册系列答案
相关题目
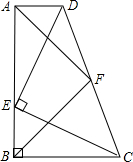 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.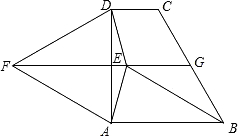 ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.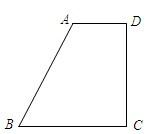 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.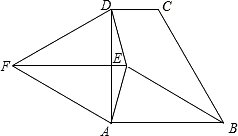 (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.