题目内容
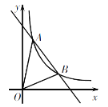
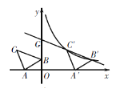
【题目】如图，在平面直角坐标系中有Rt△ABC，∠A=90°，AB=AC，A（-2，0），B（0，1），C（d，2）．
（1）求d的值；
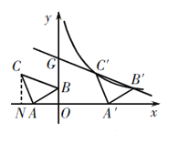
（2）将△ABC沿x轴的正方向平移，在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上． 请求出这个反比例函数和此时的直线B′C′的解析式.
【答案】（1）d=-3.（2）y=-
x+3.
【解析】
（1）过C作CN垂直于x轴，交x轴于点N，由A、B及C的坐标得出OA，OB，CN的长，再证明Rt△CNA≌Rt△AOB，由∠CAB=90°，根据全等三角形的对应边相等可得出CN=0A，AN=0B，由AN+OA求出ON的长，再由C在第二象限，可得出d的值；
（2）由第一问求出的C与B的横坐标之差为3，根据平移的性质得到纵坐标不变，故设出C′（m，2），则B′（m+3，1），再设出反比例函数解析式，将C′与B′的坐标代入得到关于k与m的两方程，消去k得到关于m的方程，求出方程的解得到m的值，即可确定出k的值，得到反比例函数解析式，设直线B′C′的解析式为y=ax+b，将C′与B′的坐标代入，得到关于a与b的二元一次方程组，求出方程组的解得到a与b的值，即可确定出直线B′C′的解析式；
（1）如图，作CN⊥x轴于点N，
在Rt△CNA和Rt△AOB中，
CN=AO=2，AC=AB，
∴Rt△CNA≌Rt△AOB（HL），
则AN=BO=1，
∴NO=AN+AO=3，且点C在第二象限，
∴d=-3.
（2）设反比例函数为y=
，点C′和B′在该反比例函数图象上，
设C′（m-3，2），则B′（m，1），
把点C′和B′的坐标分别代入y=，
得k=2m-6，k=m，
∴m=2m-6，
则k=6，m=6，
反比例函数解析式为y=
.
得点C′（3，2），B′（6，1）.
设直线C′B′的解析式为y=ax+b，
把C′、B′两点坐标代入得3a+b=2，6a+b=1，
∴解得a=-，b=3，
∴直线C′B′的解析式为y=-x+3.
