题目内容
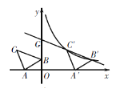
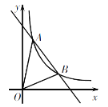
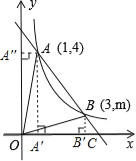
【题目】如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(1,4),B(3,m)两点.
的图象交于A(1,4),B(3,m)两点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
【答案】(1)y=﹣![]() x+
x+![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)把A代入反比例函数解析式即可求得反比例函数解析式,把点B代入反比例函数解析式就能求得完整的点B的坐标,把A,B坐标代入一次函数即可求得解析式;
(2)把三角形整理为矩形减去若干直角三角形的面积的形式,比较简便.
试题解析:(1)点A(1,4)在反比例函数y=![]() 的图象上,所以k2=xy=1×4=4,故有y=
的图象上,所以k2=xy=1×4=4,故有y=![]() 因为B(3,m)也在y=
因为B(3,m)也在y=![]() 的图象上,
的图象上,
所以m=![]() ,即点B的坐标为B(3,
,即点B的坐标为B(3,![]() ),
),
一次函数y=k1x+b过A(1,4)、B(3,![]() )两点,所以
)两点,所以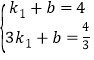
解得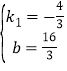 所以所求一次函数的解析式为y=﹣
所以所求一次函数的解析式为y=﹣![]() x+
x+![]()
(2)过点A分别作x轴、y轴的垂线,垂足分别为A′、A〞,过点B作x轴的
垂线,垂足为B′,
则S△AOB=S矩形OA′AA″+S梯形A′ABB′﹣S△OAA″﹣S△OBB′
=1×4+![]() ×(4+
×(4+![]() )×(3﹣1)﹣
)×(3﹣1)﹣![]() ×1×4﹣
×1×4﹣![]() ×3×
×3×![]()
=![]() ,
,
∴△AOB的面积为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目