题目内容
【题目】已知△ABC的外心为O,内心为I,∠BOC=120°,∠BIC= .
【答案】120°或150°
【解析】解:如图1,当△ABC是锐角三角形, 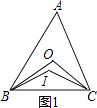
∵点O为△ABC的外心,∠BOC=120°,
∴∠A=60°,
∵点I为△ABC的内心,
∴∠ABC+∠ACB=120°,则∠IBC+∠ICB=60°,
∴∠BIC=120°.
如图2,当△ABC是钝角三角形,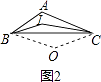
∵∠BOC=120°,
∴∠A=120°,
∴∠IBC+∠ICB=30°,
∴∠BIC=150°.
所以答案是:120°或150°.
【考点精析】掌握三角形的外接圆与外心和三角形的内切圆与内心是解答本题的根本,需要知道过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目