题目内容
【题目】![]() 与
与![]() 有公共顶点
有公共顶点![]() (顶点均按逆时针排列),
(顶点均按逆时针排列),![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
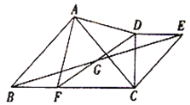
(1)如图,当![]() 时,
时,
求证:①![]() ;
;
②![]() 是等腰直角三角形.
是等腰直角三角形.
(2)当![]() 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出![]() 是何种特殊三角形.
是何种特殊三角形.
【答案】(1)①详见解析;②详见解析;(2)详见解析;
【解析】
(1)①由![]() ,
,![]() ,
,![]() 证明三角形全等,得到
证明三角形全等,得到![]() ,即可得到结论;
,即可得到结论;
②由![]() ,则
,则![]() ,然后证明
,然后证明![]() ,得到
,得到![]() ,
,![]() ,然后得到
,然后得到![]() ,即可得到结论成立;
,即可得到结论成立;
(2)根据![]() ,得到△ABC是等边三角形,由(1)可知
,得到△ABC是等边三角形,由(1)可知![]() ,得到
,得到![]() ,
,![]() ,即可判断是等边三角形.
,即可判断是等边三角形.
解:(1)证明:①∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ;
;
②当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
即![]() ,
,
∴![]() 是等腰直角三角形.
是等腰直角三角形.
(2)所画图形如图①或图②,此时![]() 是等边三角形.
是等边三角形.
图①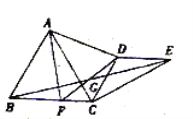
图②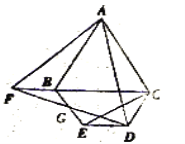
与(1)同理,可证![]() ,
,
∴AF=AD, ![]() ,
,
∴△AFD是等边三角形.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
【题目】蜀山区植物园是一座三面环水的半岛园区,拥有梅园、桂花园、竹园、木兰园、水景园等示范区。为了种植植物,需要从甲乙两地向园区A,B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A,B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需费用)。
运费(元/吨) | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
运往A、B两地的吨数 | ||
A | B | |
甲地 | x | 50-x |
乙地 | ( ) | ( ) |
(1)设甲地运往A棚营养土x吨,请用关于x的代数式完成上表;
(2)设甲地运往A棚营养土x吨,求总运费y(元)关于x(吨)的函数关系式(要求写出变量取值范围);
(3)当甲、乙两地各运往A、B两棚多少吨营养土时,总运费最省?最省的总运费是多少?



