题目内容
【题目】一个铝质的三角形框架的三边长分别为24 cm,30 cm,36 cm,要做一个与它相似的铝质三角形的框架,现有长27 cm,45 cm的两根铝材,要求以其中的一根为边,从另一根上截下两段(允许有余材),则截法有______种.
【答案】1
【解析】
先判断出两根铝材哪根为边,需截哪根,再根据相似三角形的对应边成比例求出另外两边的长,由另外两边的长的和与另一根铝材相比较即可.
∵两根铝材的长分别为27cm,45cm,若45cm为一边时,
则另两边的和为27cm,27<45,不能构成三角形,
∴必须以27cm为一边,45cm的铝材为另外两边,
设另外两边长分别为x,y,则:
若27cm与24cm相对应时,
![]() ,
,
解得:x=33.75cm,y=40.5cm,
x+y=33.75+40.5=74.25cm>45cm,故不成立,
若27cm与36cm相对应时,
![]() ,
,
解得:x=22.5cm,y=18cm,x+y=22.5+18=40.5cm<45cm,成立,
若27cm与30cm相对应时,
![]() ,
,
解得:x=32.4cm,y=21.6cm,x+y=32.4+21.6=54cm>45cm,故不成立,故只有一种截法.

【题目】数学课上,李老师出示了如下框中的题目.
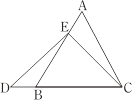
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).