题目内容
如图1,已知有一张三角形纸片ABC的一边AB=10,若D为AB边上的点,过点D作DE∥BC交AC于点E,分别过点D、E作DF⊥BC于F,EG⊥BC于G,把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠,点A、B、C分别落在A′、B′、C′处.若点A′、B′、C′在矩形DFGE内或者其边上,且互不重合,此时我们称△A′B′C′(即图中阴影部分)为“重叠三角形”.
实践探究:
(1)当AD=4时,
①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”,S△A′B′C′= ;
②若AB=AC,BC=12,如图3,S△A′B′C′= ;
③若∠B=30°,∠C=45°,如图4,S△A′B′C′= .
(2)若△ABC为等边三角形(如图5),AD=m,且重叠三角形A′B′C′存在,试用含m的代数式表示重叠三角形A′B′C′ 的面积,并写出m的取值范围.

实践探究:
(1)当AD=4时,
①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”,S△A′B′C′= ;
②若AB=AC,BC=12,如图3,S△A′B′C′= ;
③若∠B=30°,∠C=45°,如图4,S△A′B′C′= .
(2)若△ABC为等边三角形(如图5),AD=m,且重叠三角形A′B′C′存在,试用含m的代数式表示重叠三角形A′B′C′ 的面积,并写出m的取值范围.

(1)①2;② ;③
;③ ;(2)
;(2) .
.
 ;③
;③ ;(2)
;(2) .
.试题分析:(1)仔细分析题意,根据“重叠三角形”的定义结合三角形的面积公式求解即可;
(2)由AD=m可得A´D=AD=m,B´D=BD=10-m,则可得A´B´=10-2m,先证得△A´B´C´为等边三角形,根据三角形的面积公式可表示出△A´B´C´的面积,由B´C´>0 结合B´C´≤FG 即可得到关于m的不等式组,从而求得结果.
试题解析:(1)由题意得①2;②
 ;③
;③ ;
;(2)∵A’D=AD=m,B’D=BD=10-m,
∴ A’B’=10-2m
可证△A’B’C’等边三角形,
∴S△A′B′C′=
 (10-2m)2=
(10-2m)2= (5-m)2
(5-m)2由B’C’>0,得
10-2m>0,
∴m<5
由B’C’≤FG,得
10-2m≤m ,
∴m≥

∴m的取值范围为
 ≤m<5
≤m<5 
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 ,对于任意的函数值
,对于任意的函数值 ,都满足
,都满足 ,则称这个函数是有界函数,在所有满足条件的
,则称这个函数是有界函数,在所有满足条件的 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.

 和
和 是不是有界函数?若是有界函数,求其边界值;
是不是有界函数?若是有界函数,求其边界值;
 的边界值是2,且这个函数的最大值也是2,求
的边界值是2,且这个函数的最大值也是2,求 的取值范围;
的取值范围;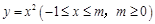 的图象向下平移
的图象向下平移 个单位,得到的函数的边界值是
个单位,得到的函数的边界值是 ,当
,当 ?
? 的方程组
的方程组
 ,求方程组的解;
,求方程组的解; ,,求
,,求 的取值范围并化简
的取值范围并化简 ;
; 的值为正整数,求整数
的值为正整数,求整数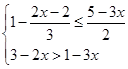
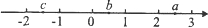
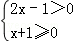 的解集是( )
的解集是( )
 ,则
,则
 ,则
,则
