题目内容
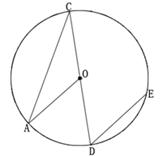
如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=400,则∠BAC的度数是( )

A 100 B 200 C 300 D 400

A 100 B 200 C 300 D 400
B
试题分析:根据切线的性质可得∠PAO=∠PBO=90°,再根据四边形的内角和为360°,即可得到∠AOB的度数,再根据等边对等角以及三角形的内角和定理求得∠BAC的度数.
∵PA、PB是⊙O的切线,A、B为切点,
∴∠PAO=∠PBO=90°,
∴∠AOB=180°-∠P=140°,
∵OA=OB,
∴∠BAC=20°,
故选B.
点评:解答本题的关键是熟练掌握切线的性质:切线垂直于过切点的半径。

练习册系列答案
相关题目
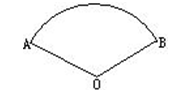
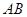 所对圆周角∠ACB的度数是( )
所对圆周角∠ACB的度数是( )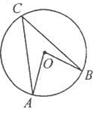
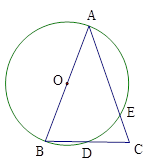
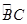 的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为 ( )
的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为 ( )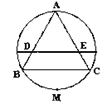
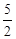
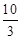
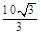
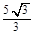
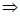 ○”表示。并证明。
○”表示。并证明。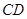 是⊙
是⊙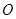 的直径过点
的直径过点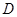 的弦,
的弦,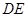 平行半径
平行半径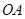 ,若∠
,若∠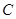 的度数是( )。
的度数是( )。