题目内容
四边形ABCD是矩形,点P是直线AD与BC外的任意一点,连接P
(1)如图(1),当点P在线段BC的垂直平分线MN上(对角线AC与BD的交点Q除外)时,证明△PAC≌△PDB;

(2)如图(2),当点P在矩形ABCD内部时,求证:PA2+PC2=PB2+PD2;

(3)若矩形ABCD在平面直角坐标系xoy中,点B的坐标为(1,1),点D的坐标为(5,3),如图(3)所示,设△PBC的面积为y,△PAD的面积为x,求y与x之间的函数关系式.
| A.P | B.P | C.P | D.请解答下列问题: |

(2)如图(2),当点P在矩形ABCD内部时,求证:PA2+PC2=PB2+PD2;

(3)若矩形ABCD在平面直角坐标系xoy中,点B的坐标为(1,1),点D的坐标为(5,3),如图(3)所示,设△PBC的面积为y,△PAD的面积为x,求y与x之间的函数关系式.

(1)证明:作BC的中垂线MN,在MN上取点P,连接PA、PB、PC、PD,

如图(1)所示,∵MN是BC的中垂线,所以有PA=PD,PC=PB,
又四边形ABCD是矩形,∴AC=DB,∴△PAC≌△PDB(SSS)
(2)证明:过点P作KG//BC ,如图(2)
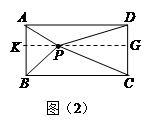
∵四边形ABCD是矩形,∴AB⊥BC,DC⊥BC
∴AB⊥KG,DC⊥KG, ∴在Rt△PAK中,PA2=AK2+PK2
同理,PC2=CG2+PG2;PB2= BK2+ PK2,PD2=+DG2+PG2
PA2+PC2= AK2+PK2+ CG2+PG2, ,PB2+ PD2= BK2+ PK2 +DG2+PG2
AB⊥KG,DC⊥KG,AD⊥AB ,可证得四边形ADGK是矩形,
∴AK=DG,同理CG="BK" ,
∴AK2=DG2,CG2=BK2
∴PA2+PC2=PB2+PD2
(3)∵点B的坐标为(1,1),点D的坐标为(5,3)
∴BC=4,AB=2 ∴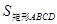 =4×2=8
=4×2=8
作直线HI垂直BC于点I,交AD于点H

①当点P在直线AD与BC之间时
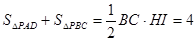
即x+y=4,因而y与x的函数关系式为y=4-x
②当点P在直线AD上方时,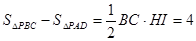
即y -x =4,因而y与x的函数关系式为y="4+x"
③当点P在直线BC下方时,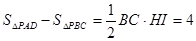
即x - y =4,因而y与x的函数关系式为y=x-4

如图(1)所示,∵MN是BC的中垂线,所以有PA=PD,PC=PB,
又四边形ABCD是矩形,∴AC=DB,∴△PAC≌△PDB(SSS)
(2)证明:过点P作KG//BC ,如图(2)
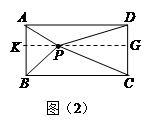
∵四边形ABCD是矩形,∴AB⊥BC,DC⊥BC
∴AB⊥KG,DC⊥KG, ∴在Rt△PAK中,PA2=AK2+PK2
同理,PC2=CG2+PG2;PB2= BK2+ PK2,PD2=+DG2+PG2
PA2+PC2= AK2+PK2+ CG2+PG2, ,PB2+ PD2= BK2+ PK2 +DG2+PG2
AB⊥KG,DC⊥KG,AD⊥AB ,可证得四边形ADGK是矩形,
∴AK=DG,同理CG="BK" ,
∴AK2=DG2,CG2=BK2
∴PA2+PC2=PB2+PD2
(3)∵点B的坐标为(1,1),点D的坐标为(5,3)
∴BC=4,AB=2 ∴
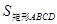 =4×2=8
=4×2=8作直线HI垂直BC于点I,交AD于点H

①当点P在直线AD与BC之间时
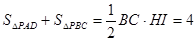
即x+y=4,因而y与x的函数关系式为y=4-x
②当点P在直线AD上方时,
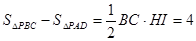
即y -x =4,因而y与x的函数关系式为y="4+x"
③当点P在直线BC下方时,
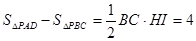
即x - y =4,因而y与x的函数关系式为y=x-4
(1)利用三角形三边关系对应相等得出△PAC≌△PDB即可;
(2)利用已知可证得四边形ADGK是矩形,进而得出 ,
, ,即可得出答案;
,即可得出答案;
(3)结合图形得出当点P在直线AD与BC之间时,以及当点P在直线AD上方时和当点P在直线BC下方时,分别求出即可.
(2)利用已知可证得四边形ADGK是矩形,进而得出
 ,
, ,即可得出答案;
,即可得出答案;(3)结合图形得出当点P在直线AD与BC之间时,以及当点P在直线AD上方时和当点P在直线BC下方时,分别求出即可.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 中,
中,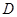 是
是 边的中点,
边的中点,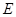 是
是 的中点,连接
的中点,连接 并延长到点
并延长到点 ,使EF=BE,连结AF、
,使EF=BE,连结AF、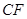 .
. 是矩形,并说明你的理由.
是矩形,并说明你的理由.

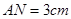 ,长
,长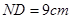 ,
, 上的点
上的点 距地面的高
距地面的高 ,地面上
,地面上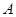 处的一只蚂蚁要到
处的一只蚂蚁要到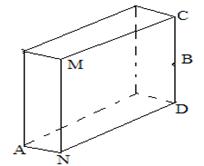
 ABCD中,AC=AD,∠B=72°,则∠CAD=_________°
ABCD中,AC=AD,∠B=72°,则∠CAD=_________°
 中,
中,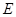 为底
为底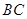 的中点,连结
的中点,连结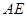 、
、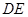 .
.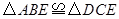 .
.