��Ŀ����
����Ŀ��һ����ѧ��������������+��������ҵ������һ�ֲ�Ʒ�����ֲ�Ʒ�ijɱ���Ϊ24Ԫ/������֪���ۼ۲����ڳɱ��ۣ�����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����32Ԫ�����г����鷢�֣��ò�Ʒÿ���������![]() ��������
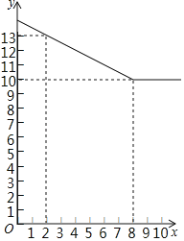
��������![]() ��Ԫ/����֮��ĺ�����ϵ��ͼ��ʾ��
��Ԫ/����֮��ĺ�����ϵ��ͼ��ʾ��
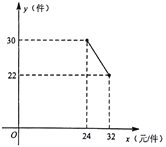
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ÿ�����������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ/����֮�ʵĺ�����ϵʽ�����ÿ�����ۼ�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��Ԫ/����֮�ʵĺ�����ϵʽ�����ÿ�����ۼ�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
���𰸡�(1)![]() ��
��![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]()
![]() ;(2)�����ۼ�Ϊ32Ԫʱ��ÿ���������������������Ϊ176Ԫ.
;(2)�����ۼ�Ϊ32Ԫʱ��ÿ���������������������Ϊ176Ԫ.
��������
(1)����ͼ����Եõ�![]() ��
��![]() ֮��ĺ�����ϵʽ��һ�κ���������֪������ȷ���ĵ�����꣬���ô���ϵ������������һ�κ����Ľ���ʽ����ͼ���ܵ�֪�Ա�����ȡֵ��Χ��
֮��ĺ�����ϵʽ��һ�κ���������֪������ȷ���ĵ�����꣬���ô���ϵ������������һ�κ����Ľ���ʽ����ͼ���ܵ�֪�Ա�����ȡֵ��Χ��
(2)������(1)��֪��Ʒÿ���������![]() ��������
��������![]() ��Ԫ/����֮��ĺ�����ϵ����������=���ۼ�-�ɱ��ۣ����������������г����̣����̵��������ۼ۵������������Ա�����ȡֵ��Χ���ɵõ��������
��Ԫ/����֮��ĺ�����ϵ����������=���ۼ�-�ɱ��ۣ����������������г����̣����̵��������ۼ۵������������Ա�����ȡֵ��Χ���ɵõ��������
�⣺(1)��![]() ��
��![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]()
������ã�![]()
��ã�![]()
��![]() ��
��![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]()
![]()
(2)![]()
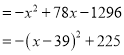
��![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
�൱![]() ʱ��
ʱ��![]() ����������Ϊ
����������Ϊ![]() Ԫ
Ԫ
��![]()
![]()
�����ۼ�Ϊ32Ԫʱ��ÿ���������������������Ϊ176Ԫ��