题目内容
【题目】如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
(1)当x=9时,求BM的长和△ABM的面积;
(2)是否存在点M,使MDDC=20?若存在,请求出x的值;若不存在,请说明理由.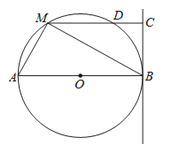
【答案】证明:(1)∵直线BC与半径为6的⊙O相切于点B,且AB为⊙O的直径,
∴AB⊥BC,
又∵MC⊥BC,
∴AB∥MC,
∴∠BMC=∠ABM,
∵AB是⊙O的直径,
∴∠AMB=90°,
∴∠BCM=∠AMB=90°,
∴△BCM∽△AMB,
∴![]() ,
,
∴BM2=ABMC=12×9=108,
∴BM=6![]() ,
,
∵BC2+MC2=BM2 ,
∴BC=![]() =3
=3![]()
∴S△ABM=![]() ABBC=
ABBC=![]() ×12×3
×12×3![]() =18
=18![]() ;
;
(2)解:过O作OE⊥MC,垂足为E,
∵MD是⊙O的弦,OE⊥MD,
∴ME=ED,
又∵∠CEO=∠ECB=∠OBC=90°,
∴四边形OBCE为矩形,
∴CE=OB=6,
又∵MC=x,
∴ME=ED=MC﹣CE=x﹣6,MD=2(x﹣6),
∴CD=MC﹣MD=x﹣2(x﹣6)=12﹣x,
∴MDDC=2(x﹣6)(12﹣x)=﹣2x2+36x﹣144=﹣2(x﹣9)2+18
∵6<x<12,
∴当x=9时,MDDC的值最大,最大值是18,
∴不存在点M,使MDDC=20.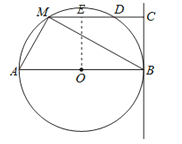
【解析】(1)利用切线的性质以及平行线的性质进而得出∠BMC=∠ABM以及∠BCM=∠AMB=90°,即可得出△BCM∽△AMB,根据相似三角形的性质即可求得BM的长,根据勾股定理求得BC,然后根据三角形面积公式求得△ABM的面积;
(2)首先得出四边形OBCE为矩形,进而得出MDDC=2(x﹣6)(12﹣x),进而求出最值即可判定
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 名校课堂系列答案
名校课堂系列答案【题目】我市某绿色无公害蔬菜基地有甲、乙两种植户,他们们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积(单位:亩) | 种植B类蔬菜面积(单位:亩) | 总收入(单位:元) |
甲 | 1 | 3 | 13500 |
乙 | 2 | 2 | 13000 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)今年甲、乙两种植户联合种植,计划合租50亩地用来种植A、B两类蔬菜,为了使总收入不低于16400元,问联合种植最多可以种植A类蔬菜多少亩?
【题目】棱长为a的小正方体,按照如图所示的方法一直维续摆放,自上而下分别叫第1层、第2层、……第n(n>0)层,第n层的小方体的个数记为S.
![]()


(1)完成下表:
n | 1 | 2 | 3 | 4 | … |
S | 1 | 3 | _____ | _____ | … |
(2)上述活动中,自变量和因变量分别是什么?
(3)研究上表可以发现S随n的增大而增大,且有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时S的值.