题目内容
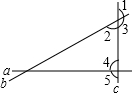
如图，直线AB、CD相交于点O，OE、OF分别平分∠BOD和∠BOC，若∠DOE=35°，求∠COF．
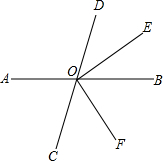
∵OE、OF分别平分∠BOD和∠BOC，
∴∠BOE=∠DOE=35°，∠BOF=∠COF，
∵直线AB、CD相交于点O，
∴∠BOE+∠DOE+∠BOF+∠COF=180°，
∴∠COF=
（180°-2×35°）=55°．
∴∠BOE=∠DOE=35°，∠BOF=∠COF，
∵直线AB、CD相交于点O，
∴∠BOE+∠DOE+∠BOF+∠COF=180°，
∴∠COF=
| 1 |
| 2 |
练习册系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
