题目内容
课本回顾
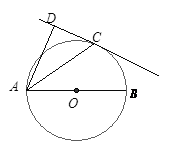
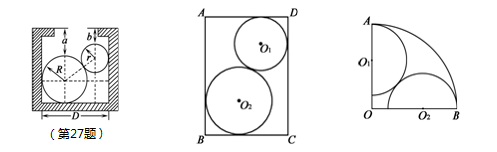
如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为 .
问题拓展
如图,在矩形ABCD内,已知⊙O1与⊙O2互相外切,且⊙O1与边AD、DC相切,⊙O2与边AB、BC相切.若AB=4,BC=3,⊙O1与⊙O2的半径分别为r,R.求O1O2的值.
灵活运用
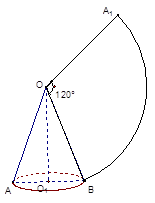
如图,某市民广场是半径为60米,圆心角为90°的扇形AOB,广场中两个活动场所是圆心在OA、OB上,且与扇形OAB内切的半圆☉O1、☉O2,其余为花圃.若这两个半圆相外切,试计算当两半圆半径之和为50米时活动场地的面积.
如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为 .
问题拓展
如图,在矩形ABCD内,已知⊙O1与⊙O2互相外切,且⊙O1与边AD、DC相切,⊙O2与边AB、BC相切.若AB=4,BC=3,⊙O1与⊙O2的半径分别为r,R.求O1O2的值.
灵活运用
如图,某市民广场是半径为60米,圆心角为90°的扇形AOB,广场中两个活动场所是圆心在OA、OB上,且与扇形OAB内切的半圆☉O1、☉O2,其余为花圃.若这两个半圆相外切,试计算当两半圆半径之和为50米时活动场地的面积.

(1)9cm;(2)7-2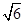 ;(3)650π平方米.
;(3)650π平方米.
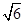 ;(3)650π平方米.
;(3)650π平方米.试题分析:(1)利用相切两圆的性质得出AB=5cm,再利用已知得出BC的长,由勾股定理求出AC的长,即可得出EF的长;
(2)连接O1、O2,并分别过O1、O2作AB、BC的平行线,则O1O22=O1 E2+O2E2,进而求出R+r的值即可;
(3)当两圆半径之和为50米时,有O1O=60-r,O2O=60-R,O1O2=50,则(60-r)2+(60-R)2=502,即可得出R2+r2,进而利用圆的面积公式求出即可.
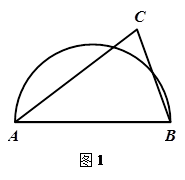
(1)如图1,
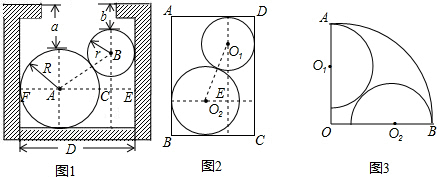
∵半径R=3cm,r=2cm,a=4cm,b=2cm,
∴AB=5cm,BC=3+4-4=3(cm),
∴AC=4cm,
∴D=EF=AF+EC+AC=3+4+2=9(cm).
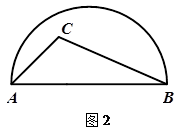
(2)如图2,连接O1、O2,并分别过O1、O2作AB、BC的平行线.
则O1O22=O1 E2+O2E2.
即(R+r)2=[4-(R+r)]2+[3-(R+r)]2
化简得:(R+r)2-14(R+r)+25=0,
解得:O1O2=r+R=7-2
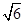 或7+2
或7+2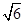 (不合题意舍去);
(不合题意舍去);(3)当两圆半径之和为50米时,
有O1O=60-r,O2O=60-R,O1O2=50,
则(60-r)2+(60-R)2=502.
即R2+r2-120(R+r)+4700=0.
∴R2+r2=1300.
∴活动场所面积=
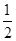 πR2+
πR2+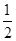 πr2=
πr2=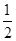 π•1300=650π(平方米).
π•1300=650π(平方米).
练习册系列答案
相关题目
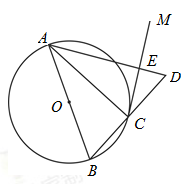
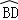 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.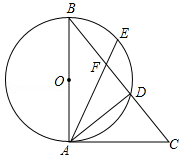
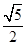 ,求AB的长.
,求AB的长.