Question

如图，已知反比例函数y=

k

x

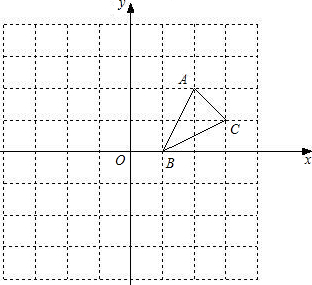
的图象经过点A（-1，3），若在x轴上存在点B，使得线段BA绕点B逆时针旋转90°后，点A仍落在反比例函数图象上，则B点的坐标为______．

Answer 1

∵反比例函数y=

k

x

的图象经过点A（-1，3），
∴

k

-1

=3，
解得k=-3，
∴反比例函数解析式为y=-

3

x

，
设OB=a，
①如图1，点B在x轴负半轴时，过点A作AC⊥x轴于C，过点A′作A′D⊥x轴于D，
∵旋转角是90°，
∴∠ABA′=90°，
∴∠ABC+∠A′BD=90°，
又∵∠BAC+∠ABC=90°，
∴∠BAC=∠A′BD，
在△ABC和△BA′D中，

∠BAC=∠A′BD ∠ACB=∠A′DB=90° AB=A′B

，
∴△ABC≌△BA′D（AAS），
∴A′D=BC=a-1，BD=AC=3，
∴点A′的坐标为（-a-3，a-1），
代入反比例函数解析式得，-

3

-a-3

=a-1，
解得a₁=-1+

7

，a₂=-1-

7

（舍去），
∴点B的坐标为（1-

7

，0），
②如图2，点B在x轴正半轴时，
同理可得点A′的坐标为（a-3，a+1），
代入反比例函数解析式得，-

3

a-3

=a+1，
解得，a₁=0（舍去），a₂=2，
∴点B的坐标为（2，0），
综上所述，点B的坐标为（1-

7

，0）或（2，0）．
故答案为：（1-

7

，0）或（2，0）．