题目内容
【题目】如图是小明设计用手电筒来测量某古城墙高度的示意图．在地面上点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB＝1.2米，BP＝1.8米，PD＝18米，那么该古城墙的高度是（ ）
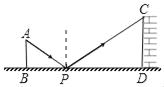
A. 6米 B. 8米 C. 12米 D. 24米
【答案】C
【解析】
由镜面反射的知识可得∠APB=∠CPD，结合∠ABP=∠CDP即可得到△ABP∽△CDP，接下来，由相似三角形的三边对应成比例可得
，至此，本题不难求解.
解：由镜面反射原理知∠APB=∠CPD.
∵AB⊥BD，CD⊥BD，
∴∠ABP=∠CDP.
∵∠ABP=∠CDP，∠APB=∠CPD，
∴△ABP∽△CDP，
∴ABBP=CDDP.
∵AB=1.2米，BP=1.8米，DP=18米，，
∴CD= 
=12（米）.
故该古城墙的高度是12米.
故选C.
【题目】2007年上海国际汽车展期间，某公司对参观本次车展盛会的且有购车意向的消费者进行了随机问卷调查，共发放900份调查问卷，并收回有效问卷750份．工作人员对有效调查问卷作了统计，其中：
①将消费者年收入的情况整理后，制成表格如下：
年收入(万元) | 4.8 | 6 | 7.2 | 9 | 10 |
被调查的消费者人数(人) | 150 | 338 | 160 | 60 | 42 |
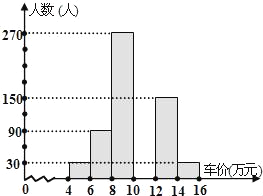
②将消费者打算购买小车的情况整理后，绘制出频数分布直方图(如图，尚未绘完整)．(注：每组包含最小值不包含最大值．)请你根据以上信息，回答下列问题：
(1)根据①中信息可知，被调查消费者的年收入的中位数是______万元．
(2)请在图中补全这个频数分布直方图．
(3)打算购买价格10万元以下(不含10万元)小车的消费者人数占被调查消费者人数的百分比是_______．
(4)本次调查的结果，是否能够代表全市所有居民的年收入情况和购车意向？为什么？
【题目】自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
（Ⅰ）写出
的值；
（Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利? 说明理由．
