题目内容
已知抛物线m:y=ax2+bx+c (a ≠ 0) 与x轴交于A、B两点(点A在左),与y轴交于点C,顶点为M,抛物线上部分点的横坐标与对应的纵坐标如下表:

1.(1)根据表中的各对对应值,请写出三条与上述抛物线m有关(不能直接出现表中各对对应值)的不同类型的正确结论;
2.(2)若将抛物线m,绕原点O顺时针旋转180°,试写出旋转后抛物线n的解析式,并在坐标系中画出抛物线m、n的草图;
3.(3)若抛物线n的顶点为N,与x轴的交点为E、F(点E、 F分别与点A、B对应),试问四边形NFMB是何种特殊四边形?并说明其理由.
1.已知抛物线m: y=ax2+bx+c (a ≠ 0) 与x轴交于A、B两点(点A在左),与y轴交于点C,顶点为M,抛物线上部分点的横坐标与对应的纵坐标如下表:

(1)根据表中的各对对应值,请写出三条与上述抛物线m
有关(不能直接出现表中各对对应值)的不同类型的正确结
论;
2.(2)若将抛物线m,绕原点O顺时针旋转180°,试写出旋转后抛物线n的解析式,并在坐标系中画出抛物线m、n的草图;
3.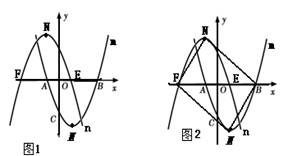 (3)若抛物线n的顶点为N,与x轴的交点为E、F
(3)若抛物线n的顶点为N,与x轴的交点为E、F
(点E、 F分别与点A、B对应),试问四边形NFMB是何种特殊四边形?并说明其理由.
答案:解:(1)答案不唯一,只要合理均可.例如:
①抛物线开口向上;
②抛物线的对称轴为x=1;③与![]() 轴的交点A坐标为(-1,0);④当x= 4时,对应的函数值y为5;⑤a=1,b=-2,c=-3或抛物线的解析式为:
轴的交点A坐标为(-1,0);④当x= 4时,对应的函数值y为5;⑤a=1,b=-2,c=-3或抛物线的解析式为:![]()
⑥抛物线的顶点M(1,-4)等. (2)抛物线m,n如图1所示, 并易得A(-1,0),B(3,0),C(0,-3),则可求得抛物线m的解析式为:![]() ,M(1,-4)抛物线n的顶点是N(-1,4),E(1,0),F(-3,0), 解析式为:
,M(1,-4)抛物线n的顶点是N(-1,4),E(1,0),F(-3,0), 解析式为:![]() 即:
即:![]()
(3)如图2,四边形NFMB是平行四边形, 理由: ∵N与M 关于原点中心对称,∴原点O是NM的中点,同理,原点O也是FB的中点.故四边形NFMB是平行四边形.
解析:略

 名校课堂系列答案
名校课堂系列答案 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-