题目内容
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.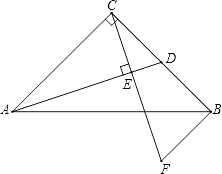
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
【答案】
(1)解:∵在Rt△ABC中,∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°,
∵CE⊥AD,
∴∠CAD=∠BCF,
∵BF∥AC,
∴∠FBA=∠CAB=45°
∴∠ACB=∠CBF=90°,
在△ACD与△CBF中,
∵ 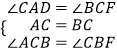 ,
,
∴△ACD≌△CBF;
(2)解:证明:∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
在△ACD与△CBF中,
∵ 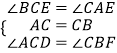 ,
,
∴△ACD≌△CBF,
∴CD=BF.
∵CD=BD= ![]() BC,
BC,
∴BF=BD.
∴△BFD为等腰直角三角形.
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分线.
∴BA是FD边上的高线,BA又是边FD的中线,
即AB垂直平分DF
【解析】(1)根据∠ACB=90°,AC=BC,求得∠CAD=∠BCF,再利用BF∥AC,求得∠ACB=∠CBF=90°,然后利用ASA即可证明△ACD≌△CBF,
(2)利用同角的余角相等得出,∠BCE=∠CAE,再根据平行线的性质得出∠ACD=∠CBF=90°,然后由ASA判定△ACD≌△CBF得到BF=BD,再根据角度之间的数量关系求出∠ABC=∠ABF,即BA是∠FBD的平分线,从而利用等腰三角形三线合一的性质求证即可
【考点精析】根据题目的已知条件,利用平行线的性质和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角).

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案