题目内容
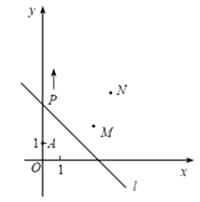
【题目】直线y=kx+b与反比例函数y=![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN=![]() ,求t的值.
,求t的值.
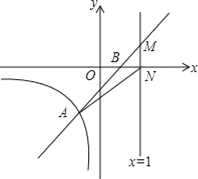
【答案】(1)﹣2;(2)y=x﹣1;(3)t=2.
【解析】试题分析:(1)将点A坐标代入y=![]() 可得m的值;
可得m的值;
(2)将点A、B坐标代入y=kx+b可得关于k、b的方程,解方程求出k、b的值,可得直线解析式;
(3)根据直线直线x=t与直线y=kx+b交于点M、与x轴交于点N表示出M、N的坐标,由S△AMN=![]() 可得关于t的方程,解方程可得t的值.
可得关于t的方程,解方程可得t的值.
解:(1)将点A(﹣1,m)代入y=![]() ,得:m=﹣2;
,得:m=﹣2;
(2)由(1)知点A坐标为(﹣1,﹣2),
将点A(﹣1,﹣2)、B(1,0)代入y=kx+b,
得: ![]() ,
,
解得: ![]() ,
,
∴直线AB的解析式为:y=x﹣1;
(3)当x=t时,y=t﹣1,
∴点M坐标为(t,t﹣1),点N坐标为(t,0),
∵S△AMN=![]() ,
,
∴![]() ×(t﹣1)(t+1)=
×(t﹣1)(t+1)=![]() ,
,
解得:t=2或t=﹣2(舍),
∴t=2.

练习册系列答案
相关题目
【题目】学校七年级学生做校服,校服分小号、中号、大号、特大号四种,随抽取若干名学生调查身高得如下统计分布表:
型号 | 身高x/cm | 人数 | 频率 |
小号 | 145≤x<155 | 20 | 0.2 |
中号 | 155≤x<165 | a | 0.45 |
大号 | 165≤x<175 | 30 | b |
特大号 | 175≤x<185 | 5 | 0.05 |
(1)这次共抽取__名学生;
(2)a=__,b=__.