题目内容
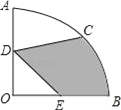
【题目】如图,在圆心角为90°的扇形OAB中,半径OA=4,C为![]() 的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为_____.
的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为_____.
【答案】2π+2![]() ﹣2
﹣2
【解析】试题分析:连接OC、作CF⊥OA,可得CF=![]() =2
=2![]() ,分别求出空白图形ACD的面积、S扇形OAB、S△ODE面积,根据S阴影部分=S扇形OBA+S空白图形ACD﹣S△ODE可得.
,分别求出空白图形ACD的面积、S扇形OAB、S△ODE面积,根据S阴影部分=S扇形OBA+S空白图形ACD﹣S△ODE可得.
解:连结OC,过C点作CF⊥OA于F,
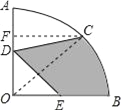
∵半径OA=4,C为![]() 的中点,D、E分别是OA、OB的中点,
的中点,D、E分别是OA、OB的中点,
∴OD=OE=2,OC=4,∠AOC=45°,
∴CF=2![]() ,
,
∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积
=![]() ﹣
﹣![]() ×2×2
×2×2![]()
=2π﹣2![]() ,
,
三角形ODE的面积=![]() OD×OE=2,
OD×OE=2,
∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积
=![]() ﹣(2π﹣2
﹣(2π﹣2![]() )﹣2
)﹣2
=2π+2![]() ﹣2.
﹣2.
故答案为:2π+2![]() ﹣2.
﹣2.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
【题目】学校七年级学生做校服,校服分小号、中号、大号、特大号四种,随抽取若干名学生调查身高得如下统计分布表:
型号 | 身高x/cm | 人数 | 频率 |
小号 | 145≤x<155 | 20 | 0.2 |
中号 | 155≤x<165 | a | 0.45 |
大号 | 165≤x<175 | 30 | b |
特大号 | 175≤x<185 | 5 | 0.05 |
(1)这次共抽取__名学生;
(2)a=__,b=__.