Question

【题目】如图，在直角坐标系，矩形OABC的边OA在x轴上，边OC在y轴上，点B的坐标为（3，1），将矩形沿对角线BO翻折，C点落在D点的位置，且BD交x轴于点E．那么点D的坐标为 ．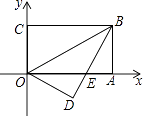

Answer 1

【答案】（ ， ）
【解析】解：如图，过D作DF⊥OC于F，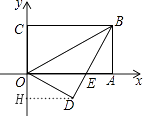
∵点B的坐标为（3，1），
∴BC=AO=3，AB=OC=1，
根据折叠可知：BD=BC=OA=3，∠ODE=∠OAB=∠OCB=90°，OD=OC=AB=1，
在△ODE和△BAE中， ，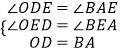
∴△ODE≌△BAE（AAS），
∴DE=AE，OE=BE，
设AE=x，那么OE=3﹣x，DE=x，
∴在Rt△ODE中，OE2=DE2+OD2 ，
∴（3﹣x）2=x2+12 ，
解得：x= ，
∴OE= ，DE= ，
又∵DF⊥OC，
∴DF∥EO，
∴∠ODF=∠EOD，
∵∠DFO=∠ODE=90°，
∴△ODF∽△DOE，∴ = =
∴OF= ，DF= ，
∴点D的坐标为（ ， ）．
根据折叠可知：BD=BC=OA=3，∠ODE=∠OAB=∠OCB=90°，OD=OC=AB=1，由AAS证明△ODE≌△BAE，得出DE=AE，OE=BE，设AE=x，那么OE=3﹣x，DE=x，在Rt△ODE中，由勾股定理得出方程，解方程求出OE= ，DE= ，证明△ODF∽△DOE，得出对应边成比例求出OF= ，DF= ，即可得出点D的坐标．