��Ŀ����
����Ŀ��ijУ���꼶��ѧ��ȤС������������ڽǻ����ƽ���ߵļн���������ڽǵ�������ϵ��������̽����
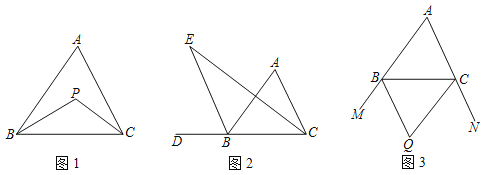
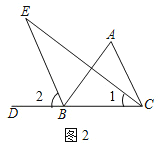
��1����ͼ1���ڡ�ABC�У���ABC���ACB��ƽ���߽��ڵ�P����A��64�������BPC���� ����
��2����ͼ2����ABC���ڽǡ�ACB��ƽ�������ABC����ǡ�ABD��ƽ���߽��ڵ�E�����С�A���������BEC����������ʾ��BEC����
��3����ͼ3����CBM����BCNΪ��ABC����ǣ���CBM����BCN��ƽ���߽��ڵ�Q������д����BQC���A��������ϵ����֤����
���𰸡���1����BPC��122������2����BEC��![]() ����3����BQC��90����
����3����BQC��90����![]() ��A��֤��������
��A��֤��������
��������
��1�����������ε��ڽǺͻ�Ϊ��ƽ���ߵĶ��壻
��2�����������ε�һ����ǵ������������ڵ������ڽǵĺͣ��á�A���1��ʾ����2�������á�E���1��ʾ����2�����ǵõ����ۣ�
��3�����������ε�һ����ǵ������������ڵ������ڽǵĺ��Լ���ƽ���ߵĶ����ʾ����EBC���ECB��Ȼ���ٸ��������ε��ڽǺͶ�����ʽ�������ɵý⣮
�⣺��1��![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]()
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�
![]() ��
��![]() ��
��
��![]() ��
��![]() ��һ��ǣ�
��һ��ǣ�
![]() ��
��
![]() ��
��
![]() ��
��![]() ��һ��ǣ�
��һ��ǣ�
![]() ��
��
��3��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
���ۣ�![]() ��
��

 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�����Ŀ����ͼ����ABC�У�AB=BC=5cm��AC=6cm����P�Ӷ���B��������B��C��A��ÿ��1cm���ٶ������˶���A�㣬���˶�ʱ��Ϊx�룬BP����Ϊycm��ijѧϰС��Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽�������������ǵ�̽�����̣��벹��������
��1��ͨ��ȡ�㣬��ͼ���������õ���x���룩��y��cm���ļ����Ӧֵ��
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.5 | 4.1 | 4 | 4.5 | 5.0 |
Ҫ��ȫ�����������ֵ������һλС������
��2����ƽ��ֱ������ϵ�У�����Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
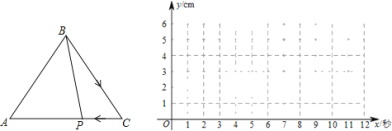
��3����ϻ����ĺ���ͼ������⣺��xԼΪ______ʱ��BP=CP��
����Ŀ������Լ�������������ѡ��������2%��Χ֮�ڶ���Ϊ����������������Ϊ���˽�ijУ���꼶�����о������ձ������������������ǴӸ�У���꼶������������10���������ֱ���������ǵ�����(��λ��cm)���ռ�����������ͳ�Ʊ���
���� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� |
����x(cm) | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
����������Ϣ������������⣺
(1)�����������ݵ�����ͳ������ƽ��������λ����������
(2)����ѡ������һ��ͳ������Ϊѡ�������ҳ���10�������о������ձ����������ļ�λ��������˵�����ɣ�