题目内容
【题目】为了保护环境,新农村改造过程中需要修建污水处理厂,如图,![]() 、
、![]() 是位于直线小河
是位于直线小河![]() 同侧的两个村庄,
同侧的两个村庄,![]() 村距离小河
村距离小河![]() 的距离
的距离![]() ,
,![]() 村距离小河
村距离小河![]() 的距离
的距离![]() ,经测量
,经测量![]() ,现准备在小河边修建一个污水处理厂
,现准备在小河边修建一个污水处理厂![]() .(不考虑河宽)
.(不考虑河宽)
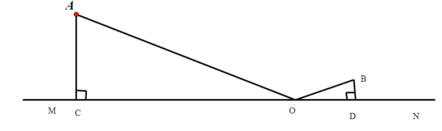
(1)设![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长(保留根号);
的长(保留根号);
(2)为了节省材料,使得两村的排污管道最短,求最短的排污管长;
(3)根据(1)(2)的结果,运用数形结合思想,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)25米;(3)17
;(2)25米;(3)17
【解析】
(1)根据勾股定理即可得到结论;
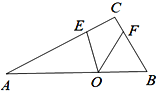
(2)作点A关于直线MN的对称点A′,连接A′B交MN于O,此时,OA+OB=OB+OA′的长最短,即点O即为污水处理厂的位置,根据勾股定理即可得到结论;
(3)由(2)可知,作出图形,利用最短路径问题和勾股定理解题,即可得到答案.
解:(1)在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() .
.
(2)作点![]() 关于
关于![]() 对称点为
对称点为![]() ,可以得到,
,可以得到,![]() .
.
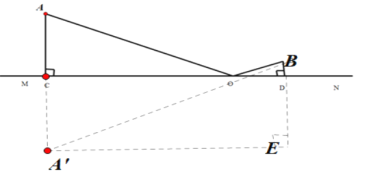
根据两点之间线段最短可以得到,![]() 的长度就是最短的排污管.
的长度就是最短的排污管.
∵![]() ,
,![]() ,
,
由勾股定理得:![]() .
.
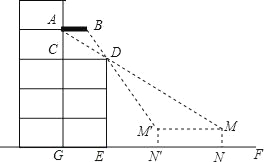
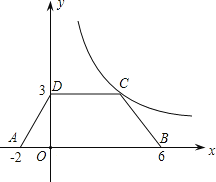
(3)根据(2)的结果,先作对称点,把问题转化到求最短距离问题.如图:
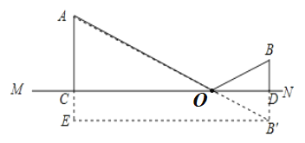
设BD=2,AC=6,CD=15,设OC=a,则OD=15-a,
根据勾股定理得,AO+OB=![]() ,
,
此时![]() ,
,
当A、O、B′三点共线时,OA+OB的值最小,
∴![]() 的值最小,即
的值最小,即![]() 的长度;
的长度;
∴最小值为:![]() ;
;
∴![]() 的最小值为17.
的最小值为17.

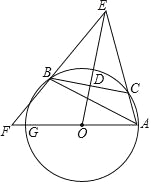
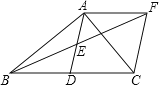
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.