Question

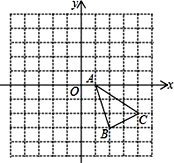
【题目】在平面直角坐标系中，点A（2，0），B（0，4），若以B，O，C为顶点的三角形与△ABO全等，则点C的坐标不能为（　　）

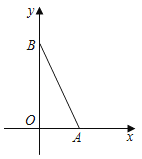
A.（0，﹣4）B.（﹣2，0）C.（2，4）D.（﹣2，4）

Answer 1

【答案】A

【解析】

根据全等三角形的判定定理画图并逐一判断即可.

解:如图所示:

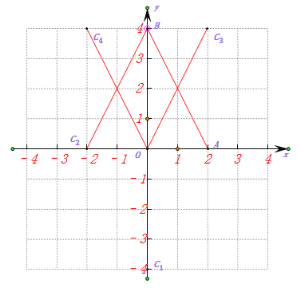
∵A（2，0），B（0，4）

∴OA=2，OB=4，∠AOB=90°

当C1坐标为（0，﹣4）时,B、O、C1同一条直线上，不能构成三角形，故选A；

当C2坐标为（﹣2，0）时，OC2= OA=2，∠C2O B =∠AOB=90°，OB=OB

∴△C2O B≌△AOB，故不选B；

当C3坐标为（2，4）时，BC3= OA=2，∠C3 B O =∠AOB=90°，OB=BO

∴△C3BO≌△AOB，故不选C；

当C4坐标为（﹣2，4）时，BC4= OA=2，∠C4BO =∠AOB=90°，OB=BO

∴△C4BO≌△AOB，故不选D.

故选A.