题目内容
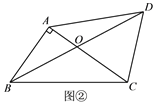
【题目】如图,在ABCD中,E为边AB上一点,连结DE,将ABCD沿DE翻折,使点A的对称点F落在CD上,连结EF.
(1)求证:四边形ADFE是菱形.
(2)若∠A=60°,AE=2BE=2.求四边形BCDE的周长.
小强做第(1)题的步骤
解:①由翻折得,AD=FD,AE=FE.
②∵AB∥CD.
③∴∠AED=∠FDE.
④∴∠AED=∠ADE
⑤∴AD=AE
⑥∴AD=AE=EF=FD
∴四边形ADFE是菱形.
(1)小强解答第(1)题的过程不完整,请将第(1)题的解答过程补充完整(说明在哪一步骤,补充什亻么条件或结论)
(2)完成题目中的第(2)小题.

【答案】(1)见解析;(2)四边形BCDE的周长为8.
【解析】
(1)由题意可知,第一步补充∠ADE=∠FDE.
(2)由平行四边形的性质和菱形的性质可得,BE,BC,CD,DE的长度,即可求四边形BCDE的周长
解:(1)①由翻折得,AD=FD,AE=FE.(补充∠ADE=∠FDE)
②∵AB∥CD
③∴∠AED=∠FDE.
④∴∠AED=∠ADE
⑤∴AD=AE
⑥∴AD=AE=EF=FD
∴四边形ADFE是菱形.
(2)∵AE=2BE=2
∴BE=1
∴AB=CD=3
∵AD=AE,∠A=60°∴△ADE是等边三角形∴AD=DE=2
∴AD=BC=2
∴四边形BCDE的周长=BE+DE+CD+BC=1+2+3+2=8.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工时,检修小组在![]() 地的何方向?距离
地的何方向?距离![]() 地多远?
地多远?
(2)在第几次纪录时距![]() 地最远?
地最远?
(3)若汽车行驶每千米耗油0.4升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?