题目内容
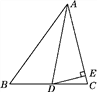
【题目】在△ABC中,AD是角平分线,∠B=54°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
【答案】(1) 101°,79°;(2)14°.
【解析】试题分析:(1)、首先根据三角形内角和定理求出∠BAC的度数,根据角平分线的性质求出∠BAD和∠DAC的度数,然后根据三角形内角和定理得出∠ADB和∠ADC的度数;(2)、根据垂直得出∠AED=90°,然后根据外角的性质求出∠EDC的度数.
试题解析:(1)、∵∠B=54°,∠C=76° , ∴∠BAC=180°-54°-76°=50°,
∵AD是角平分线, ∴∠BAD=∠DAC=25°,
∴∠ADB=180°-54°-25°=101°,∠ADC=180°-76°-25°=79°;
(2)、∵DE⊥AC,∴∠AED=90°,∴∠EDC=90°-76°=14°.

【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试,计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,达到9分或10分为优秀,成绩如表1所示,并制作了成绩分析表(表2)
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | b | c | 10 | 4.94 | 80% | 40% |
(1)求表2中,a,b,c;
(2)有人说二班的及格率、优秀率均高于一班,所以二班成绩比一班成绩好;但也有人坚定认为一班成绩比二班成绩好.请你给出支持一班成绩好的两条理由.
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?