题目内容
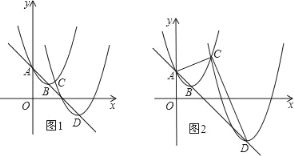
【题目】如图1,已知直线l:y=﹣x+2与y轴交于点A,抛物线y=(x﹣1)2+m也经过点A,其顶点为B,将该抛物线沿直线l平移使顶点B落在直线l的点D处,点D的横坐标n(n>1).
(1)求点B的坐标;
(2)平移后的抛物线可以表示为 (用含n的式子表示);
(3)若平移后的抛物线与原抛物线相交于点C,且点C的横坐标为a.
①请写出a与n的函数关系式.
②如图2,连接AC,CD,若∠ACD=90°,求a的值.
【答案】(1)B(1,1);(2)y=(x﹣n)2+2﹣n.(3)a=![]() ;a=
;a=![]() +1.
+1.
【解析】
1) 首先求得点A的坐标, 再求得点B的坐标, 用h表示出点D的坐标后代入直线的解析式即可验证答案。
(2) ①根据两种不同的表示形式得到m和h之间的函数关系即可。
②点C作y轴的垂线, 垂足为E, 过点D作DF⊥CE于点F, 证得△ACE~△CDF, 然后用m表示出点C和点D的坐标, 根据相似三角形的性质求得m的值即可。
解:(1)当x=0时候,y=﹣x+2=2,
∴A(0,2),
把A(0,2)代入y=(x﹣1)2+m,得1+m=2
∴m=1.
∴y=(x﹣1)2+1,
∴B(1,1)
(2)由(1)知,该抛物线的解析式为:y=(x﹣1)2+1,
∵∵D(n,2﹣n),
∴则平移后抛物线的解析式为:y=(x﹣n)2+2﹣n.
故答案是:y=(x﹣n)2+2﹣n.
(3)①∵C是两个抛物线的交点,
∴点C的纵坐标可以表示为:
(a﹣1)2+1或(a﹣n)2﹣n+2
由题意得(a﹣1)2+1=(a﹣n)2﹣n+2,
整理得2an﹣2a=n2﹣n
∵n>1
∴a=![]() =
=![]() .
.
②过点C作y轴的垂线,垂足为E,过点D作DF⊥CE于点F
∵∠ACD=90°,
∴∠ACE=∠CDF
又∵∠AEC=∠DFC
∴△ACE∽△CDF
∴![]() =
=![]() .
.
又∵C(a,a2﹣2a+2),D(2a,2﹣2a),
∴AE=a2﹣2a,DF=m2,CE=CF=a
∴![]() =
=![]()
∴a2﹣2a=1
解得:a=±![]() +1
+1
∵n>1
∴a=![]() >
>![]()
∴a=![]() +1
+1

 高中必刷题系列答案
高中必刷题系列答案