题目内容
【题目】如图,抛物线y=﹣![]() (x﹣k)2+
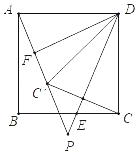
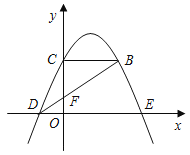
(x﹣k)2+![]() 经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
(1)求点E的坐标.
(2)求△CFB的面积.
【答案】(1)E(3,0);(2)![]() .
.
【解析】
(1)把点D(-1,0)代入y=﹣![]() (x﹣k)2+
(x﹣k)2+![]() ,求k=1,令y=0 有0=﹣
,求k=1,令y=0 有0=﹣![]() (x﹣k)2+
(x﹣k)2+![]() ,解得x1=-1,x2=3,即可求解;
,解得x1=-1,x2=3,即可求解;
(2)求出BD的解析式:![]() ,OF=
,OF=![]() CF=
CF=![]() ,△CFB的面积=
,△CFB的面积=![]() .
.
(1)把点D(﹣1,0)代入y=﹣![]() (x﹣k)2+
(x﹣k)2+![]() ,
,
解得:k=1;
∴y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
令y=0,有![]() ,解得x1=﹣1,x2=3,
,解得x1=﹣1,x2=3,
∴点E(3,0);
(2)令x=0时,y=2,
当y=2时,有![]()
解得x1=0,x2=2,
点B的坐标为:(2,2),点D(﹣1,0),
设直线BD的解析式为y=mx+n,
将点B、D的坐标代入一次函数表达式并解得:
直线BD的解析式为:![]() ,
,
∴OF=![]() ,CF=
,CF=![]() ,
,
△CFB的面积=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目