题目内容
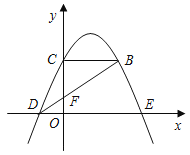
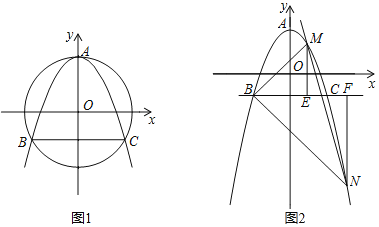
【题目】已知抛物线y=ax2+bx+c过顶点A(0,2),以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.
(1)求抛物线的解析式.
(2)若MN与直线y=﹣2![]() x平行,M(x1,y1),N(x2,y2),M,N都在抛物线上,且M,N位于直线BC的两侧,y1>y2,ME⊥BC于E,NF⊥BC于F,解决以下问题:
x平行,M(x1,y1),N(x2,y2),M,N都在抛物线上,且M,N位于直线BC的两侧,y1>y2,ME⊥BC于E,NF⊥BC于F,解决以下问题:
①求证:![]() .
.
②求△MBC外心的纵坐标的取值范围.
【答案】(1)抛物线解析式为y=﹣x2+2;(2)①证明见解析;②﹣![]() <y0≤0.
<y0≤0.
【解析】
(1)由顶点坐标为(0,2)可得c=2,由对称轴为y轴可得b=0,△ABC为等腰三角形,根据有一个角是60°可得△ABC是等边三角形,设线段BC与y轴的交点为点D,连接OB,根据垂径定理可得BD=CD,根据外心的定义可得∠OBD=30°,利用∠OBD的正弦和余弦值可求出OD和BD的长,即可得得B坐标,代入抛物线解析式可求出a值,即可得答案;(2)①根据MN与y=﹣2![]() x平行设直线MN的解析式为y=﹣2
x平行设直线MN的解析式为y=﹣2![]() x+m,把M点坐标代入可得m=﹣x12+2
x+m,把M点坐标代入可得m=﹣x12+2![]() x1+2,即可得出MN的解析式,代入y=﹣x2+2可用x1表示出x2,进而可表示出y2,分别用x1表示出∠MBE和∠NBF的正切函数即可得结论;②过M作ME⊥y轴于E,由y轴为BC的垂直平分线,可知△NBC的外心在y轴上,设外心P坐标为(0,y0),可得PB=PM,利用勾股定理可用y1表示出y0,根据y1的取值范围即可得答案.
x1+2,即可得出MN的解析式,代入y=﹣x2+2可用x1表示出x2,进而可表示出y2,分别用x1表示出∠MBE和∠NBF的正切函数即可得结论;②过M作ME⊥y轴于E,由y轴为BC的垂直平分线,可知△NBC的外心在y轴上,设外心P坐标为(0,y0),可得PB=PM,利用勾股定理可用y1表示出y0,根据y1的取值范围即可得答案.
(1)∵抛物线过点A(0,2),
∴c=2,
∴抛物线的对称轴为y轴,且开口向下,即b=0,
∵以O为圆心,OA为半径的圆与抛物线交于另两点B,C,y轴为抛物线对称轴,
∴B、C关于y轴对称,
∴△ABC为等腰三角形,
∵△ABC中有一个角为60°,
∴△ABC为等边三角形,且OC=OA=2,
设线段BC与y轴的交点为点D,连接OB,
∵AD⊥BC,AD过圆心,
∴BD=CD,
∵O为△ABC的外心,△ABC为等边三角形,
∴∠OBD=30°,
∴BD=OBcos30°=![]() ,OD=OBsin30°=1,
,OD=OBsin30°=1,
∵B在C的左侧,
∴B的坐标为(﹣![]() ,﹣1),
,﹣1),
∵B点在抛物线上,且c=2,b=0,
∴3a+2=﹣1,
解得:a=﹣1,
则抛物线解析式为y=﹣x2+2.
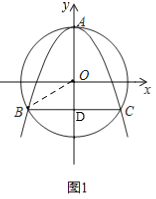
(2)①由(1)知,点M(x1,﹣x12+2),N(x2,﹣x22+2),
∵MN与直线y=﹣2![]() x平行,
x平行,
∴设直线MN的解析式为y=﹣2![]() x+m,
x+m,
∴﹣x12+2=﹣2![]() x1+m,即m=﹣x12+2
x1+m,即m=﹣x12+2![]() x1+2,
x1+2,
∴直线MN解析式为y=﹣2![]() x﹣x12+2
x﹣x12+2![]() x1+2,
x1+2,
把y=﹣2![]() x﹣x12+2
x﹣x12+2![]() x1+2代入y=﹣x2+2,
x1+2代入y=﹣x2+2,
解得:x=x1或x=2![]() ﹣x1,
﹣x1,
∴x2=2![]() ﹣x1,即y2=﹣(2
﹣x1,即y2=﹣(2![]() ﹣x1)2+2=﹣x12+4
﹣x1)2+2=﹣x12+4![]() x1﹣10,
x1﹣10,
如图2所示,作ME⊥BC,NF⊥BC,垂足为E,F,
∵M,N位于直线BC的两侧,且y1>y2,
∴y2<﹣1<y1≤2,且﹣![]() <x1<x2,
<x1<x2,
∴ME=y1﹣(﹣1)=﹣x12+3,BE=x1﹣(﹣![]() )=x1+
)=x1+![]() ,
,
NF=﹣1﹣y2=x12﹣4![]() x1+9,BF=x2﹣(﹣
x1+9,BF=x2﹣(﹣![]() )=3
)=3![]() ﹣x1,
﹣x1,
在Rt△BEM中,tan∠MBE=![]() =
=![]() =
=![]() ﹣x1,
﹣x1,
在Rt△BFN中,tan∠NBF=![]() =
=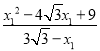
=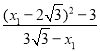
=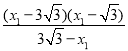
=![]() -x1,
-x1,
∴![]() =
=![]() .
.
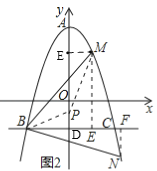
②过M作ME⊥y轴于E,
∵y轴为BC的垂直平分线,
∴设△MBC的外心为P(0,y0),则PB=PM,即PB2=PM2,
∵B的坐标为(﹣![]() ,﹣1),
,﹣1),
∴PD=y0+1,PD=![]() ,ME=x1,PE=y1﹣y0,
,ME=x1,PE=y1﹣y0,
根据勾股定理得:3+(y0+1)2=x12+(y1﹣y0)2,
∵x12=2﹣y1,
∴y02+2y0+4=(2﹣y1)+(y0﹣y1)2,即y0=![]() y1﹣1,
y1﹣1,
由①得:﹣1<y1≤2,
∴﹣![]() <y0≤0,
<y0≤0,
则△MBC的外心的纵坐标的取值范围是﹣![]() <y0≤0.
<y0≤0.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案