题目内容
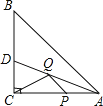
【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=2![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F
(1)求∠ABE的度数;
(2)用这个扇形AFED围成一个圆锥的侧面,所得圆锥的底面半径是多少?

【答案】(1)45°;(2)0.75.
【解析】连接AE,因为BC为圆A的切线,所以AE垂直于BC,所以三角形ABE为直角三角形,所以三角形ABE为等腰直角三角形,所以∠BAE为45°,因为∠AEB为直角,且AD平行于BC,所以∠DAE等于∠AEB等于90°,所以圆心角BAD等于45+90等于135°,弧FED的长等于![]() 乘以2π乘以2,等于1.5π,而扇形DAF为圆锥的侧面,所以弧长为圆锥的底面圆的周长,所以半径等于周长除以2π,所以半径等于0.75.
乘以2π乘以2,等于1.5π,而扇形DAF为圆锥的侧面,所以弧长为圆锥的底面圆的周长,所以半径等于周长除以2π,所以半径等于0.75.
解:(1)连接AE,如图1,

∵AD为半径的圆与BC相切于点E,
∴AE⊥BC,AE=AD=2.在Rt△AEB中,∵AB=2![]() , AE =2,由勾股定理得AE=BE,
, AE =2,由勾股定理得AE=BE,
∴∠ABE=45°.
(2)∵AD∥BC,
∴∠DAE=∠AEB=90°,
∴∠BAD45°+90°=135°,
∴扇形A-BFE的弧长=![]() =
=![]() .
.
设所得圆锥的底半径是r,
则2πr=![]() ,
,
∴r=0.75.
即:所得圆锥的底面半径是0.75.
“点睛”此题考查了切线的性质、直角三角形全等的判定与性质、等腰直角三角形的性质以及弧长公式.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目