题目内容
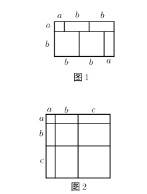
【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数 ![]() (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 ![]() 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
【答案】
(1)证明:∵三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,
∴重新排序后:其中两个数位上数字的和是一个数位上的数字的2倍,
∴a+c﹣2b=0,即(a﹣b)﹣(b﹣c)=0,
∴F(t)=0;
(2)解:∵m=200+10x+y是“善雅数”,
∴x为偶数,且2+x+y是3的倍数,
∵x<10,y<10,
∴2+x+y<30,
∵m的各位数字之和为一个完全平方数,
∴2+x+y=32=9,
∴当x=0时,y=7,
当x=2时,y=5,
当x=4时,y=3,
当x=6时,y=1,
∴所有符合条件的“善雅数”有:207,225,243,261,
∴所有符合条件的“善雅数”中F(m)的最大值是)=|2﹣4|﹣|4﹣3|=1.
【解析】(1)由三位正整数中,有一个数位上的数字是另外两数位上的数字的平均数,根据最优组合的定义即可求解;
(2)由三位“善雅数”的定义,可得a为偶数,且2+x+y是3的倍数,且2+x+y<30,又有m的各位数字之和为一个完全平方数,可得2+x+y=32=9,继而求得答案。

【题目】“PM2.5”指数是空气中可入肺颗粒物的含量,是空气质量的指标之一.下表为A市1﹣12月“PM2.5月平均指数”(单位:微克/立方米)
PM2.5指数 | 20 | 30 | 40 | 41 | 43 | 50 |
月数 | 2 | 4 | 3 | 1 | 1 | 1 |
(1)求这12个月“PM2.5月平均指数”的众数、中位数、平均数;
(2)根据《环境空气质量标准》,宜居城市的标准之一是“PM2.5年平均指数少于35微克/立方米”,请你判断A市是否为宜居城市?