题目内容
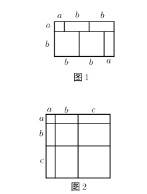
【题目】如图1,小明用1张边长为![]() 的正方形,2张边长
的正方形,2张边长![]() 为的正方形,3张边长分别为
为的正方形,3张边长分别为![]() 的长方形纸片拼成一个长为
的长方形纸片拼成一个长为![]() ,宽为
,宽为![]() 的长方形,它的面积为
的长方形,它的面积为![]() ,于是,我们可以得到等式
,于是,我们可以得到等式![]()
请解答下列问题:
(1)根据图2,写出一个代数恒等式;
(2)利用(1)中所得的结论,解决下面的问题:已知![]() ,求
,求![]() 的值.
的值.
(3)小明又用4张边长为![]() 的正方形,3张边长为
的正方形,3张边长为![]() 的正方形,8张边长分别为
的正方形,8张边长分别为![]() 的长方形纸片拼出一个长方形,那么该长方形的长为__________,宽为__________;
的长方形纸片拼出一个长方形,那么该长方形的长为__________,宽为__________;
【答案】(1)![]() ;(2)30;(3)
;(2)30;(3)![]() 或
或![]() ;
;![]() 或
或![]()
【解析】
(1)先从整体表达出正方形的总面积:![]() ,各个小的矩形的面积之和为:
,各个小的矩形的面积之和为:![]() ,总的正方形的面积等于各个小的矩形面积之和,即可得出答案;
,总的正方形的面积等于各个小的矩形面积之和,即可得出答案;
(2)利用(1)中所得的结论和已知条件:![]() ,进行整体运算即可得到结果;
,进行整体运算即可得到结果;
(3)根据题意可知拼出的长方形的总面积为:![]() ,再用因式分解法即可求出答案.
,再用因式分解法即可求出答案.
(1)根据总的正方形的面积等于各个小的矩形面积之和可得:
![]() ;
;
(2)由(1)可知:![]()
将![]() 代入上式,
代入上式,
可得:![]() ,
,
则![]() ,
,
故![]() ;
;
(3)根据题意可知拼出的长方形的总面积为:![]() ,
,
根据因式分解法可得:
![]() ,
,
故根据几何意义可得:
该长方形的长为![]() 或
或![]() ,宽为
,宽为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】一股民在上星期五买进某公司股票1000股,每股27元,下表为本星期内每日该股票的涨跌情况![]() 单位:元
单位:元![]()
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股多少元?
星期三收盘时,每股多少元?
![]() 本星期内每股最低价多少元?
本星期内每股最低价多少元?
![]() 本周星期几抛售,获利最大,最大是多少?
本周星期几抛售,获利最大,最大是多少?