题目内容
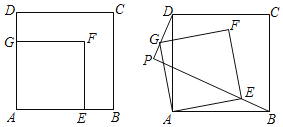
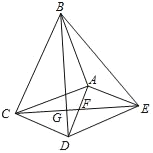
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,CE交AD于点F,交BD于点G.甲,乙两位同学对条件进行分折后,甲得到结论:“CE=BD”.乙得到结论:“CDAE=EFCG”请判断甲,乙两位同学的结论是否正确,并说明理由.
【答案】甲,乙两位同学的结论正确.理由见解析.
【解析】
利用SAS证明△BAD≌△CAE,可得到CE=BD;利用已知得出∠GFD=∠AFE,以及∠GDF+∠GFD=90°,得出∠GCD=∠AEF,进而得出△CGD∽△EAF,得出比例式;即可得出结论.
甲,乙两位同学的结论正确.
理由:∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即:∠BAD=∠CAE,
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∴△BAD≌△CAE(SAS),
∴CE=BD,
故甲正确
∵△BAD≌△CAE,△BAE≌△BAD,
∴△CAE≌△BAE,
∴∠BEA=∠CEA=∠BDA,
∵∠AEF+∠AFE=90°,
∴∠AFE+∠BEA=90°,
∵∠GFD=∠AFE,∠ADB=∠AEB,
∴∠ADB+∠GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△EAF,
∴![]() ,
,
∴CDAE=EFCG.
故乙正确.

练习册系列答案
相关题目