题目内容
【题目】如图,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=![]() ,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
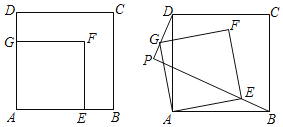
(1)∠BPD=______度;
(2)点P所经过的路径长为______.
【答案】90. ![]()
【解析】
(1)根据正方形性质证△EAB≌△GAD(SAS),得∠ABE=∠ADG,由∠ABE+∠AOB=90°,∠AOB=∠DOP,得∠DOP+∠ADG=90°;(2)当P、G重合时,作AH⊥BG于H.点P经过路径是图中弧AG.根据三角函数知识,求出∠ABH=30°,∠AOG=2∠ABG=60°,![]() 的长=
的长=![]() .
.
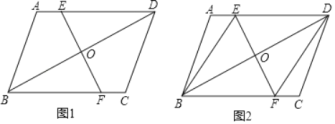
解:(1)如图1中,设AD交PB于点O.
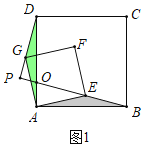
∵四边形ABCD,四边形AEFG都是正方形,
∴AB=AD,AE=AG,∠DAB=∠GAE,
∴∠EAB=∠GAD,
∴△EAB≌△GAD(SAS),
∴∠ABE=∠ADG,
∵∠ABE+∠AOB=90°,∠AOB=∠DOP,
∴∠DOP+∠ADG=90°,
∴∠BPD=90°.
故答案为90.
(2)如图2中,当P、G重合时,作AH⊥BG于H.
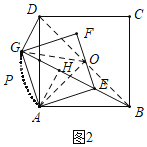
∵∠BPD=90°,
∴点P经过路径是图中弧AG.
∵AE=AG=1,∠EAG=90°,
∴EG=![]() ,
,
∵AH⊥EG,
∴HG=HE,
∴AH=![]() ,
,
∴sin∠ABH=![]() ,
,
∴∠ABH=30°,
∴∠AOG=2∠ABG=60°,
∴![]() 的长=
的长=![]() .
.
故答案为![]() .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】为了打造书香城市,截止2019年3月洛阳市有17家河洛书苑书房对社会免费开放.某书房为了解读者阅读的情况,随机调查了部分读者在一周内借阅图书的次数,并制成如图不完整的统计图表.
读者借阅图书的次数统计表
借阅图书的次数 | 1次 | 2次 | 3次 | 4次 | 5次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)这组数据的众数为 ,中位数为 ;
(3)请计算扇形统计图中的“4次”所对应的圆心角的度数;
(4)据统计该书房一周共有2000位不同的读者,根据以上调查结果,请你计算出一周内借阅图书“4次及以上”的读者人数.