题目内容
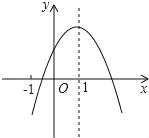
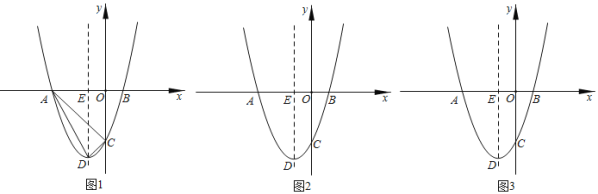
【题目】在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴的交点为
轴的交点为![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,其对称轴与
,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求二次函数解析式;
(2)连接![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)点![]() 为第三象限内抛物线上一点,
为第三象限内抛物线上一点,![]() 的面积记为
的面积记为![]() ,求
,求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
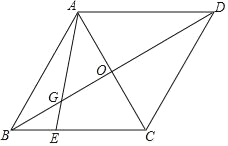
(4)在线段![]() 上,是否存在点
上,是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 为直角三角形,理由见解析;(3)当
为直角三角形,理由见解析;(3)当![]() 时,
时,![]() ,此时
,此时![]() ;(4)
;(4)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)二次函数表达式为:y=a(x+3)(x-1)=a(x2+2x-3),则-3a=-3,解得:a=1,即可求解;
(2)由AD2=AC2+CD2,故△ADC为直角三角形;
(3)![]()
![]()
![]()
![]() .,即可求解;
.,即可求解;
(4)分AE=EF、AE=AF、AF=EF三种情况分别求解即可.
(1)设![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴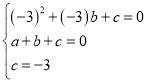 ,
,
∴ ,
,
∴二次函数解析式为:![]() .
.
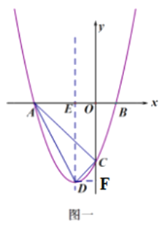
(2)![]() 为直角三角形,理由:
为直角三角形,理由:
由(1)可知![]() ,
,
过点![]() 作
作![]() 轴于
轴于![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() 为直角三角形.
为直角三角形.
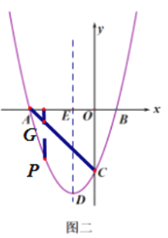
(3)设直线![]() 解析式为:
解析式为:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于
于![]() ,设
,设![]() ,
,
则![]() .
.
∵点![]() 在第三象限,
在第三象限,
∴![]()
![]()
![]() ,
,
∴![]()
![]()
![]()
![]() .
.
∴当![]() 时,
时,![]() ,此时
,此时![]() .
.
(4)![]() ,
,![]() ,
,![]() .理由如下:
.理由如下:
∵OA=OC=3,∴∠OAC=∠OCA=45°,
①当AE=EF时,如下图,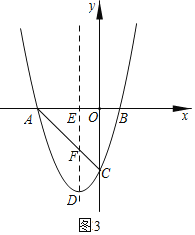
△AEF为等腰直角三角形,AE=2=EF,
∴点F(-1,2);
②当AE=AF时,
同理可得:点F(![]() -3,-
-3,-![]() );
);
③当AF=EF时,
同理可得:点F(-2,-1);
故点F的坐标为:![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目