��Ŀ����
����Ŀ����֪���κ���y��ax��x��3��+c��a��0��0��x��3��������������y��![]() ��x��0��k��0��ͼ����ͼ1��ʾ����������y��
��x��0��k��0��ͼ����ͼ1��ʾ����������y��![]() ��x��0��k��0����ͼ����P��m��n����PM��x�ᣬ����ΪM��PN��y�ᣬ����ΪN����OM��ON��12����1����k��ֵ��
��x��0��k��0����ͼ����P��m��n����PM��x�ᣬ����ΪM��PN��y�ᣬ����ΪN����OM��ON��12����1����k��ֵ��
��2��ȷ�����κ���y��ax��x��3��+c��a��0��0��x��3���Գ��ᣬ�����㵱aȡ��1ʱ���κ��������ֵ�����ú�����ĸc��ʽ�ӱ�ʾ��
��3����c��0ʱ��������������x�����������֮��ľ��룮
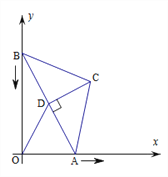
��4����ͼ2����a��1ʱ��������y��ax��x��3��+c��a��0��0��x��3����һʱ��ǡ�þ���P�㣬�Ҵ�ʱ��������˫����y��![]() ��x��0��k��0������ֻ��һ��������P����ͼ2��ʾ�������Dz����Ѵ�ʱ�̵�c����c1����ֱ��д��������y��ax��x��3��+c��a��0��0��x��3����ͼ����˫����y��
��x��0��k��0������ֻ��һ��������P����ͼ2��ʾ�������Dz����Ѵ�ʱ�̵�c����c1����ֱ��д��������y��ax��x��3��+c��a��0��0��x��3����ͼ����˫����y��![]() ��x��0��k��0����ͼ����һ��������ʱc��ȡֵ��Χ��
��x��0��k��0����ͼ����һ��������ʱc��ȡֵ��Χ��

���𰸡�(1)k��12����2 x��![]() �����ֵΪ
�����ֵΪ![]() +c����3��3����4����������
+c����3��3����4����������
��������
��1����OM��ON=12����k=OM��ON��������⣻
��2��y=ax��x-3��+c�ĶԳ���Ϊx=![]() =
=![]() ����a=-1ʱ������y=ax��x-3��+c=-x��x-3��+c��������⣻
����a=-1ʱ������y=ax��x-3��+c=-x��x-3��+c��������⣻
��3����c=0ʱ����ʱ��y=0����ax��x-3��=0����a��0x��x-3��=0��������⣻
��4����c��c1��c=c1��c��c1��c��4����������ֱ���⼴�ɣ�
�⣺��1����OM��ON��12����k��OM��ON��12��
��2��y��ax��x��3��+c�ĶԳ���Ϊx����![]() ��
��![]() ��
��
��a����1ʱ������y��ax��x��3��+c����x��x��3��+c��
��y����x2��3x+c������x+![]() ��2+
��2+![]() +c��
+c��
���ʱ���κ���y����x��x��3��+c��a��0��0��x��3�������ֵΪ![]() +c��
+c��
��3����c��0ʱ�����κ���y��ax��x��3��+c��ax��x��3����a��0��0��x��3����
��ʱ��y��0����ax��x��3����0����a��0x��x��3����0��
��x��0��3��
����κ���y��ax��x��3����x�����������Ϊ��0��0���ͣ�3��0����
����������x�����������֮��ľ���Ϊ3��
��4���ٵ�c��c1ʱ��
������y����x��x��3��+c��ͼ����˫����y��![]() û�й����㣻
û�й����㣻
�ڵ�c��c1ʱ��
������y����x��x��3��+c��a��0��0��x��3����ͼ����˫����y��![]() ��Ψһ������P��
��Ψһ������P��
�۵�c��c1ʱ��
����������ƽ�ƣ����������Ҷ˵���������˫������ʱ���������ʱ��B������Ϊ��3��c1����c1��4��
�൱c1��c��4ʱ����������˫���������������㣻
�ܵ�c��4ʱ��������y����x��x��3��+c��a��0��0��x��3����ͼ���˫����ʼ����һ�������㣻
���Ե�c��c1ʱ��c��4ʱ��������y����x��x��3��+c��a��0��0��x��3����ͼ���˫����ʼ����һ�������㣮

 �����ܿ����ϵ�д�
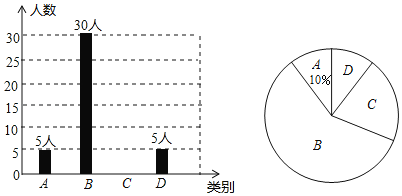
�����ܿ����ϵ�д�����Ŀ��Ϊ�˴���������У���ֹ2019��3����������17�Һ�����Է�鷿�������ѿ��ţ�ij�鷿Ϊ�˽�����Ķ����������������˲��ֶ�����һ���ڽ���ͼ��Ĵ��������Ƴ���ͼ��������ͳ��ͼ����
���߽���ͼ��Ĵ���ͳ�Ʊ�
����ͼ��Ĵ��� | 1�� | 2�� | 3�� | 4�� | 5�μ����� |
���� | 7 | 13 | a | 10 | 3 |
�������ͳ��ͼ���е���Ϣ������������⣺
��1��a���� ����b���� ����
��2���������ݵ�����Ϊ�� ������λ��Ϊ�� ����
��3�����������ͳ��ͼ�еġ�4�Ρ�����Ӧ��Բ�ĽǵĶ�����
��4����ͳ�Ƹ��鷿һ�ܹ���2000λ��ͬ�Ķ��ߣ��������ϵ���������������һ���ڽ���ͼ�顰4�μ����ϡ��Ķ���������