题目内容
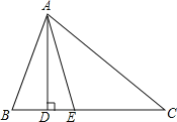
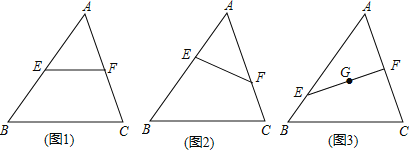
【题目】(1)(发现)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.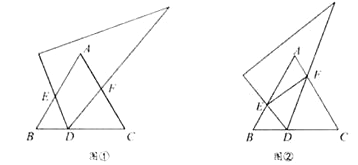
①若AB=6,AE=4,BD=2,则CF =________;
②求证:△EBD∽△DCF.
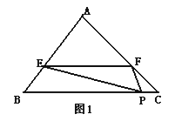
(2)(思考)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示.问点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
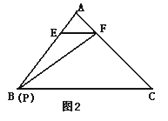
(3)(探索)如图③,在等腰△ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________(用含α的表达式表示)
.
【答案】(1)①4;②证明见解析;(2)存在;(3)1-cosα.
【解析】(1)①先求出BE的长度后发现BE=BD,又∠B=60°,可知△BDE是等边三角形,可得∠BDE=60°,另外∠EDF=60°,可证得△CDF是等边三角形,从而CF=CD=BC-BD;
②证明△EBD∽△DCF,这个模型可称为“一线三等角相似模型”,根据“AA”判定相似;
(2)【思考】由平分线可联系到角平分线的性质“角平分线上的点到角两边的距离相等”,可过D作DM⊥BE,DG⊥EF,DN⊥CF,则DM=DG=DN,从而通过证明△BDM△CDN可得BD=CD;
(3)【探索】由已知不难求得C△ABC=AB+BC+CA=2AB+2OB=2(m+mcosα),则需要用m和α的三角函数表示出C△AEF,C△AEF=AE+EF+AF;题中直接已知O是BC的中点,应用(2)题的方法和结论,作OG⊥BE,OD⊥EF,OH⊥CF,可得EG=ED,FH=DF,则C△AEF=AE+EF+AF= AG+AH=2AG,而AG=AB-OB,从而可求得.
(1)①∵△ABC是等边三角形,
∴AB=BC=AC=6,∠B=∠C=60°,
∵AE=4,
∴BE=2,则BE=BD,
∴△BDE是等边三角形,
∴∠BDE=60°,
又∵∠EDF=60°,
∴∠CDF=180°-∠EDF-∠B=60°,则∠CDF =∠C=60°,
∴△CDF是等边三角形,
∴CF=CD=BC-BD=6-2=4;
②证明:∵∠EDF=60°,∠B=60°
∴∠CDF+∠BDE=120°,∠BED+∠BDE=120°,
∴∠BED=∠CDF,
又∵∠B=∠C,
∴△EBD∽△DCF
(2)存在.如图,作DM⊥BE,DG⊥EF,DN⊥CF,垂足分别为M,G,N,
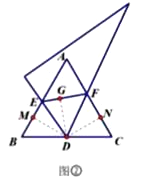
∵ED平分∠BEF且FD平分∠CFE,
∴DM=DG=DN,
又∵∠B=∠C=60°,∠BMD=∠CND=90°,
∴△BDM△CDN,
∴BD=CD,
即点D是BC的中点,
∴![]() ;
;
( 3 )连结AO,作OG⊥BE,OD⊥EF,OH⊥CF,垂足分别为G,D,H,
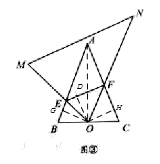
则∠BGO=∠CHO=90°,
∵AB=AC,O是BC的中点
∴∠B=∠C,OB=OC,
∴△OBG△OCH,
∴OG=OH,GB=CH,∠BOG=∠COH=90°α,
则∠GOH=180°-(∠BOG+∠COH)=2α,
∵∠EOF=∠B=α,
则∠GOH=2∠EOF=2α,
由(2)题可猜想应用EF=ED+DF=EG+FH,
则 C△AEF=AE+EF+AF=AE+EG+FH+AF=AG+AH=2AG,
设AB=m,则OB=mcosα,GB=mcos2α,
![]() .
.