题目内容
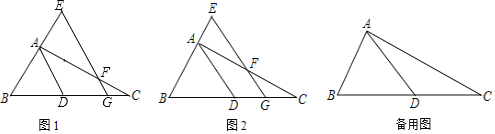
【题目】如图,已知![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 延长线上一点过点
延长线上一点过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .连结
.连结![]() ,
,![]() ,
,![]() ,
,![]() .若
.若![]() ,
,![]() .
.
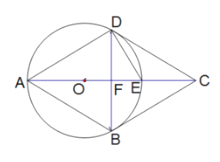
(1)求![]() 的长。
的长。
(2)求证:![]() 是
是![]() 的切线.
的切线.
(3)试判断四边形![]() 的形状,并求出四边形
的形状,并求出四边形![]() 的面积.
的面积.
【答案】(1)BD=2![]() ;(2)见解析;(3)四边形ABCD是菱形,理由见解析. 菱形ABCD得面积为6
;(2)见解析;(3)四边形ABCD是菱形,理由见解析. 菱形ABCD得面积为6![]() .
.
【解析】
(1)根据题意连结BD,利用切线定理以及勾股定理进行分析求值;
(2)根据题意连结OB,利用垂直平分线性质以及切线定理进行分析求值;
(3)由题意可知四边形ABCD是菱形,结合勾股定理利用菱形的判定方法进行求证.
解:(1)连结BD
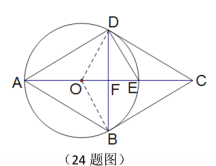
![]() DE=CE
DE=CE
∴∠DCE=∠EDC
∵⊙O与CD相切于点D,
∴OD⊥DC,∠ODC=90°
![]() ∠ODE+∠CDE=90°
∠ODE+∠CDE=90°
![]() ∠DOC+∠DCO=90°,∠DCE=∠EDC
∠DOC+∠DCO=90°,∠DCE=∠EDC
![]() ∠ODE=∠DOE
∠ODE=∠DOE
![]() DE=OE
DE=OE
∵ 在⊙O中,OE=OD
![]() OE=OD=DE
OE=OD=DE
![]() ∠DOE=60°
∠DOE=60°
∵ 在⊙O中,AE⊥DB
![]() BD=2DF
BD=2DF
∵在Rt△COE中,∠ODF-90°-∠DOE=90°-60°=30°
∴OD=2OF
∵EF=1 ,设半径为R,
![]() OF=OE-FE=R-1
OF=OE-FE=R-1
∴R=2(R-1),解得R=2
∴ ![]()
![]() BD=2DF=2
BD=2DF=2![]()
(2)连结OB
∵ 在⊙O中,AE⊥DB
![]() BF=DF
BF=DF
![]() AC是DB的垂直平分线
AC是DB的垂直平分线
∴OD=0B,CD=CB
∴∠ODB=∠OBD,∠CDB=∠CBD
∴∠ODB+∠CDB=∠OBD+∠CBD
即∠ODC=∠OBC
由(1)得∠ODC=90°
∴∠OBC=90°
即OB⊥BC
又![]() OB是⊙O的半径
OB是⊙O的半径
∴CB是⊙O的切线
(3)四边形ABCD是菱形,理由如下
∵ 由(1)得在⊙O中,∠DOE=60°,∠ODC=90°
∴∠DAO=![]() ∠DOE=30°
∠DOE=30°
∵ 由(1)得∠ODC=90°/p>
∴∠OCD=90°-∠DOC=90°-60°=30°
∴∠DAO=∠OCD
∴DA=CD
∵ 由(2)得AD=AB,CD=BC
∴AD=DC=BC=AB
∴四边形ABCD是菱形
∵在Rt△AFD中,DF=![]() ,∠DAC=30°
,∠DAC=30°
∴AD=2DF=2![]()
![]()
∵四边形ABCD是菱形
∴AC=2AF=6,BD=2DF=2![]()
∴菱形ABCD得面积为:![]() ×AC×DB=
×AC×DB=![]() ×6×2
×6×2![]() =6
=6![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】北京市第十五届人大常委会第十六次会议表决通过《关于修改<北京市生活垃圾管理条例>的决定》,规定将生活垃圾分为厨余垃圾、可回收物、有害垃圾、其它垃圾四大基本品类,修改后的条例将于2020年5月1日实施 .某小区决定在2020年1月到3月期间在小区内设置四种垃圾分类厢:厨余垃圾、可回收物、有害垃圾、其它垃圾,分别记为A、B、C、D,进行垃圾分类试投放,以增强居民垃圾分类意识.
(1)小明家按要求将自家的生活垃圾分成了四类,小明从分好类的垃圾中随机拿了一袋,并随机投入一个垃圾箱中,请用画树状图的方法求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区四类垃圾箱中共1 000千克生活垃圾,数据统计如下(单位:千克):
A | B | C | D | |
厨余垃圾 | 400 | 100 | 40 | 60 |
可回收物 | 25 | 140 | 20 | 15 |
有害垃圾 | 5 | 20 | 60 | 15 |
其它垃圾 | 25 | 15 | 20 | 40 |
求“厨余垃圾”投放正确的概率.