题目内容
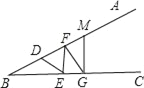
【题目】如图,平行于y轴的直尺(一部分)与双曲线y= ![]() (k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.
(k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.
(1)求k的值;
(2)求经过A、C两点的直线的解析式;
(3)连接OA、OC,求△OAC的面积.
【答案】
(1)
解:∵AB=5﹣2=3cm,OB=2cm,
∴A的坐标是(2,3),
代入y= ![]() 得3=
得3= ![]() ,
,
解得:k=6
(2)
解:OD=2+2=4,
在y= ![]() 中令x=4,解得y=
中令x=4,解得y= ![]() .
.
则C的坐标是(4, ![]() ).
).
设AC的解析式是y=mx+n,
根据题意得: 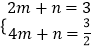 ,
,
解得: 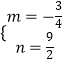 ,
,
则直线AC的解析式是y=﹣ ![]() x+
x+ ![]()
(3)
解:直角△AOB中,OB=2,AB=3,则S△AOB= ![]() OBAB=
OBAB= ![]() ×2×3=3;
×2×3=3;
直角△ODC中,OD=4,CD= ![]() ,则S△OCD=
,则S△OCD= ![]() ODCD=
ODCD= ![]() ×4×
×4× ![]() =3.
=3.
在直角梯形ABDC中,BD=2,AB=3,CD= ![]() ,则S梯形ABDC=
,则S梯形ABDC= ![]() (AB+DC)BD=
(AB+DC)BD= ![]() (3+
(3+ ![]() )×2=
)×2= ![]() .
.
则S△OAC=S△AOB+S梯形ABDC﹣S△OCD=3+ ![]() ﹣3=
﹣3= ![]()
【解析】(1)首先求得A的坐标,然后利用待定系数法求得函数的解析式;(2)首先求得C的坐标,然后利用待定系数法求得直线的解析式;(3)根据S△OAC=S△AOB+S梯形ABDC﹣S△OCD利用直角三角形和梯形的面积公式求解.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目